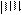Упражнение 2. Определение постоянной решетки.
Подготовить таблицу экспериментальных данных: Таблица 2. Запись результатов измерений при определении неизвестного периода решетки.
1. Выполнить все пункты упр.1, поместив на столик гониометра дифракционную решетку с неизвестным периодом d и выразив его из формулы dsinφ = kλ. 2. Заполнить табл.2, где во втором столбце записать полученные значения длины волны λ; в первом упражнении. Погрешность в определении постоянной решетки Δ d найти по вышеуказанной формуле.
Контрольные вопросы. 1. Что такое дифракция света? 2. Метод зон Френеля. 3. Дифракция на щели и препятствии. 4. Ход луча в дифракционной решетке. 5. Условия максимумов и минимумов. 6. От чего зависит угол дифракции? 7. Порядок следования цветов в спектрах от дифракционной решетки. 8. Гониометр. 9. Разрешающая способность оптических приборов. 10.Спектр видимого и солнечного света.
Литература. 1. Курс физики //под ред. В.Н.Лозовского.- С-Пб., изд. Лань, 2001 2. Ландсберг Г.С. Оптика.- М., Гостехиздат, 1979. 3. Иверонова В.И. Физический практикум.- М., Наука, 1963.
ПРИЛОЖЕНИЕ 1 Метод зон Френеля
Френель предложил рассчитать освещенность в точке пространства М от источника S при дифракции на отверстии ВВ следующим методом. Рассмотрим простейший случай – источник S, центр отверстия O и точка M лежат на одной прямой. В противном случае расчет сильно усложняется, хотя смысл остается тем же. От источника S свет распространяется сферическими волнами. В некий момент времени фронт волны доходит до отверстия ВВ и имеет вид сферического сегмента. В последующем каждая точка этого сегмента посылает свои вторичные волны, которые и дойдут до точки М. Наименьшее расстояние проходит луч из центра сегмента О. Разбиваем поверхность сегмента на зоны, точки на границе между которыми находятся на расстоянии до точки М на половину длины волны (+ λ/2) дальше, чем у предыдущей границы. Тогда свет от предыдущего и последующего зон до точки М доходят в противофазе и взаимно гасят друг друга. Амплитуду света от первой зоны Френеля обозначим А1, второй А1 , i-ой - Аi, n-ой - Аn. Учитывая, что интенсивности соседних зон приблизительно равны, оцениваем результирующую амплитуду: А = А1 – А2 + А3 – А4 + А5 ….± Аn = =А1/2 + (А1/2 – А2/2) – (А2/2 – А3/2) + (А3/2 – А4/2) –….± (Аn-1/2 – Аn/2).± Аn/2 ≈; ≈; А1/2 .± Аn/2. Знак перед Аn/2 зависит от четности: если n - четное, то минус, а если n - нечетное, то плюс. Поэтому, если от точки М в отверстии видно четное количество зон Френеля, то имеем минимум – темную точку. А =А1/2 – Аn/2, амплитуды вычитаются. Если от точки М в отверстии видно нечетное количество зон Френеля, то имеем максимум – светлую точку. А =А1/2 .+ Аn/2, амплитуды складываются. На рисунке точку М освещают три зоны Френеля, значит, имеем светлую точку. При дифракции на препятствии (диске) из-за препятствия видна первой какая-то n -ая зона Френеля, а последняя ∞-ая. Тогда в точке М на осевой линии всегда светлое пятно: А ≈; Аn/2 .± А∞/2 ≈; Аn/2, так как А∞/2 ≈; 0.
ПРИЛОЖЕНИЕ 2 Нониус лимба гониометра
Лимб гониометра разделен на 360º (градусов), а каждый градус разделен на половины градуса. Шкала гониометра снабжена нониусом, цена деления которого равна 1’ – одной минуте. 1 градус равен 60 минутам, которые в свою очередь делятся еще на 60 секунд: 1º = 60’ = 3600”.
Рис.5б. Основная шкала гониометра показывает 8º + полградуса с лишним. Нониус дает совпадение по вертикали 10-ой риски с риской на основной шкале. Поэтому снимаем показание: 8º30’+ 10’ = 8º40’
              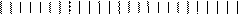 Рис.5в. Основная шкала гониометра показывает 351º + полградуса с лишним. Нониус дает совпадение по вертикали 25-ой риски с риской на основной шкале. Поэтому снимаем показание: 351º30’+ 25’ = 351º55’. Это значение можно записать как отрицательный угол = - 8º05’. Рис.5в. Основная шкала гониометра показывает 351º + полградуса с лишним. Нониус дает совпадение по вертикали 25-ой риски с риской на основной шкале. Поэтому снимаем показание: 351º30’+ 25’ = 351º55’. Это значение можно записать как отрицательный угол = - 8º05’.
|

 (мкм)
(мкм)

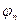

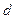 (мм)
(мм)

 Рис.5a. Основная шкала гониометра показывает 10º с лишним (по риске «0» нониуса). Нониус дает совпадение по вертикали 8-ой риски с риской на основной шкале. Поэтому снимаем показание: 10º08’
Рис.5a. Основная шкала гониометра показывает 10º с лишним (по риске «0» нониуса). Нониус дает совпадение по вертикали 8-ой риски с риской на основной шкале. Поэтому снимаем показание: 10º08’