Основное уравнение молекулярно-кинетической теории идеальных газов.
Газ, заключенный в сосуд, оказывает давление на его стенки. Это давление - результат столкновений молекул со стенками. При каждом столкновении изменяется импульс молекулы, следовательно, на нее со стороны стенки действует сила. По третьему закону Ньютона на стенку со стороны молекулы действует такая же, но противоположно направленная сила. Статистически усредняя эту силу по времени и по всем молекулам, можно получить уравнение, связывающее давление газа со средней кинетической энергией поступательного движения его молекул. Вывод этого уравнения проводится в предположении, что газ не находится во внешнем силовом поле. Следовательно, давление на все стенки сосуда одинаково. Кроме того, учитываются столкновения только со стенками сосуда. Влиянием столкновений молекул между собой, как показал Д. К. Максвелл, можно пренебречь. Основное уравнение молекулярно-кинетической теории газов имеет вид
где Средняя кинетическая энергия поступательного движения молекул найдется как
Из основного уравнения и уравнения Клапейрона-Менделеева следует, что
Тогда
где m0- масса одной молекулы. Таким образом, средняя кинетическая энергия поступательного движения молекул газа прямо пропорциональна его термодинамической температуре. Из этого выражения следует, что при Скорости различных молекул газа различны. Для характеристики средней быстроты движения молекул вводится понятие средней квадратичной скорости, определяемой как
Для среднеквадратичной скорости можно получить выражения
Например, молекулы водорода H2 при Т = 300 К в соответствии с этими выражениями имеют среднюю квадратичную скорость порядка 2•103 м/с.
|

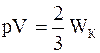 ,
,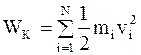 - суммарная кинетическая энергия поступательного движения всех N молекул газа,
- суммарная кинетическая энергия поступательного движения всех N молекул газа, 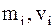 - масса и скорость i-ой молекулы.
- масса и скорость i-ой молекулы.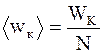 .
.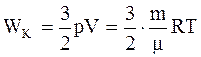 .
.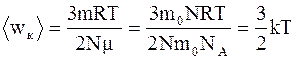 ,
,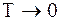
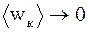 . Однако, в области сверхнизких температур неприменимы выводы классической физики. Там действуют законы квантовой статистики. Поэтому данное соотношение верно только при температурах далеких от 0 К.
. Однако, в области сверхнизких температур неприменимы выводы классической физики. Там действуют законы квантовой статистики. Поэтому данное соотношение верно только при температурах далеких от 0 К. .
.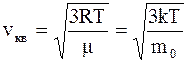 .
.


