Прогнозирование в распределительной логистике
При планировании и управлении логическими активностями часто используются различные методы и модели прогнозирования. От точности и достоверности прогнозов потребительского спроса, расходования материальных ресурсов, уровня запасов и т.п. напрямую зависит эффективность реализации практически всех логистических концепций, особенно JIT, DDT. С наиболее общих позиций прогноз — это вероятностное суждение о состоянии логистического процесса, системы или отдельных элементов в определенный момент в будущем и (или) альтернативных путях достижения этого состояния. Прогнозирование является неотъемлемой частью различных видов логистического планирования: стратегического, тактического, оперативного. Являясь средством научного обоснования плана, прогноз должен содержать необходимую информацию для планирования, включать вероятную оценку характера развития процесса логистического менеджмента и возможного пути реализации целей, поставленных перед ЛС. Экономический прогноз позволяет установить возможные направления и различные варианты развития ЛС, а также помогает в выборе конкретных целей ее функционирования. Поэтому основное назначение прогноза в логистике состоит в раскрытии тенденции изменения микро - и макрологистической среды и получения вероятностных количественных и качественных оценок динамики логистических активностей, необходимых персоналу менеджмента фирмы. Логистические менеджеры распределения в своей практической деятельности используют различные методы прогнозирования в зависимости от требуемой точности (достоверности), объема и вида исходной информации и других факторов, причем в большинстве случаев для этой цели применяются стандартные или индивидуальные компьютерные программы. Основной сферой приложения этих методов в логистике является прогнозирование спроса и объем продаж готовой продукции. Сегодня в логистической практике широко используются такие методы прогнозирования, как: простейшая модель экстраполяции тренда, адаптивные полиномиальные модели Брауна в различных вариациях, авторегрессионные модели, экспертные прогностические модели и другие. Каждый из перечисленных методов прогнозирования имеет преимущества и недостатки. Понятно, что одинаковые прогнозы получить посредством различных методов практически невозможно. Поэтому, если прогнозные значения, полученные разными методами, не совпадают, необходимо использовать их комбинацию. Для получения комбинированной оценки прогноза на первом этапе необходимо с помощью известных вероятностных критериев отбросить те прогнозные оценки, которые не согласовываются с другими. Далее с целью совместной обработки оставшихся оценок прогноза для каждого из них следует найти вес метода прогнозирования. Чем менее точен результат прогноза, тем меньше его вес в комбинированном прогнозе. Весовые коэффициенты для каждого метода можно найти в их комбинации по следующей формуле (19):
где j - количество методов, участвующих в комбинированном прогнозе.
Если в комбинированном прогнозе участвуют два метода, то по формуле (19) можно рассчитать весовые коэффициенты для каждого метода, и они будут равняться:
После установления весовых коэффициентов можем рассчитать уточненное значение прогнозированного показателя, как средневзвешенное из всех комбинаций, то есть
где
Очевидно, что среднеквадратическая ошибка комбинированного прогноза будет равняться:
Таким образом, осуществляется комбинированный прогноз интересующего нас процесса. Рассмотрим демонстрационный пример. Пример. На основании ретроспективной информации необходимо произвести прогнозирование объемов сбыта для фирмы на 2013 год с использованием двух моделей (линейный тренд и тренд параболы 2-ого порядка). Исходная информация приводится в табл. 5.1. Таблица 5.1 Исходные данные
В качестве конкурирующих моделей взять линейный тренд и параболический тренд. Решение: По условиям задачи в качестве конкурирующих моделей взяты линейный тренд
Таблица 5.2 Вычисление коэффициентов нормальных уравнений для линейного тренда
Для нахождения неизвестных параметров моделей необходимо воспользоваться системой нормальных уравнений, представленной в виде формулы:
На основании таблицы 4.7 система уравнений (4.9) примет следующий вид:
После решения этой системы, были определены числовые значения параметров: Для получения параметров параболического тренда предварительные вычисления сведем в таблицу(5.3).
Таблица 5.3 Вычисление коэффициентов нормальных уравнений для параболического тренда
Для нахождения неизвестных параметров моделей необходимо воспользоваться системой нормальных уравнений, представленной в виде формулы:
На основании таблицы 5.3 система уравнений (5.7) примет следующий вид:
После решения этой системы, были определены числовые значения параметров: Для повышения точности прогноза следует применить комбинированный прогноз. Для этого по формулам (20) и (21) необходимо найти веса для каждого прогноза. Вес для первого метода прогнозирования будет равняться:
На основании таблиц 5.2, 5.3 необходимо рассчитать дисперсии для каждого метода прогнозирования, которые будут равняться соответственно: Далее по формуле (22) необходимо найти комбинированный прогноз показателя: Для большей точности прогноза нужно произвести интервальное прогнозирование. Для этого находится интервал прогноза по формуле 25:
где l - коэффициент доверия к прогнозу, рассчитываемый на основании таблиц теории вероятностей с доверительной вероятностью (см. приложение В). В экономических исследованиях в качестве доверительной вероятности, как правило, берут 0,95; Таким образом, среднеквадратическая ошибка комбинированного прогноза в данном случае будет равняться: Далее нужно найти границы прогнозируемого показателя по формуле 26:
Подставляя данные, выражение (26) примет вид: Итак, на основании интервального комбинированного прогнозирования можно сделать вывод о том, что с доверительной вероятностью 0,95, можно утверждать, что объем реализации продукции фирмы в 2012 году будет больше 17,691 млн. руб., но и не меньше 15,865 млн. руб., если не произойдут резкие непредвиденные изменения в экономической среде в целом и на анализируемом рынке в частности.
|

 (19)
(19) - среднеквадратическая ошибка i -го метода прогноза;
- среднеквадратическая ошибка i -го метода прогноза; , (20)
, (20) , (21)
, (21) , (22)
, (22) - результат j -го прогноза.
- результат j -го прогноза. , (21)
, (21)
 и параболический тренд
и параболический тренд  . В этих выражениях
. В этих выражениях  - определяемые параметры трендовых моделей;
- определяемые параметры трендовых моделей;  - текущий номер уровня динамического ряда. Предварительные вычисления приведем в виде табл. 5.2.
- текущий номер уровня динамического ряда. Предварительные вычисления приведем в виде табл. 5.2.

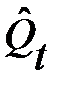


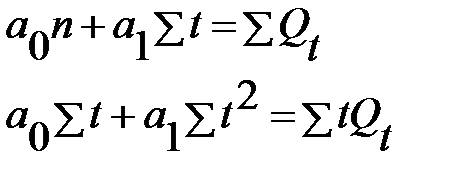 , (22)
, (22) .
. . Следовательно, модель тренда примет следующий вид:
. Следовательно, модель тренда примет следующий вид:  . На основании этой модели можно получить прогнозное значение объема реализации на 2013 год. Для этого в модель вместо
. На основании этой модели можно получить прогнозное значение объема реализации на 2013 год. Для этого в модель вместо  необходимо подставить время упреждения
необходимо подставить время упреждения  . В результате чего было получено прогнозное значение показателя для первой модели
. В результате чего было получено прогнозное значение показателя для первой модели 


 , (23)
, (23)
 . Тогда модель тренда примет следующий вид:
. Тогда модель тренда примет следующий вид:  . На основании этой модели можно получить прогнозное значение объема реализации на 2013 год. Для этого в модель вместо
. На основании этой модели можно получить прогнозное значение объема реализации на 2013 год. Для этого в модель вместо  необходимо подставить время упреждения
необходимо подставить время упреждения 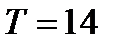 . В результате чего было получено прогнозное значение показателя для второй модели составит:
. В результате чего было получено прогнозное значение показателя для второй модели составит: 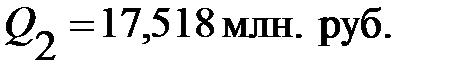
 , а для второго метода прогнозирования -
, а для второго метода прогнозирования -  . Здесь
. Здесь  и
и  - дисперсии соответственно для первого и второго методов прогнозирования, которые можно рассчитать по формуле 24:
- дисперсии соответственно для первого и второго методов прогнозирования, которые можно рассчитать по формуле 24: , (24)
, (24)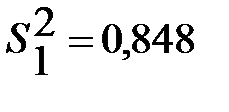 ,
,  . Следовательно, веса методов прогнозирования будут равны соответственно:
. Следовательно, веса методов прогнозирования будут равны соответственно:  и
и  .
.
 , (25)
, (25) . Коэффициент доверия к комбинированному прогнозу, который соответствует доверительной вероятности 0,95, определим по таблице (приложение В) и равняется 1,96. Тогда интервал прогноза будет равен:
. Коэффициент доверия к комбинированному прогнозу, который соответствует доверительной вероятности 0,95, определим по таблице (приложение В) и равняется 1,96. Тогда интервал прогноза будет равен:  .
. , (26)
, (26) .
.


