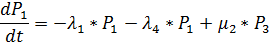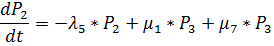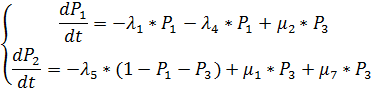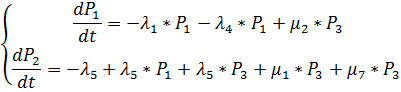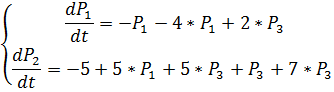Задача №6
Задача №1
Интенсивность отказов имеет вид λ(t)=at.
Найти плотность распределения наработки на отказ f(t) -? Решение: P(t)=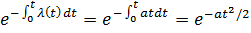 
f(t)=λ(t)*P(t)=at  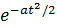=(1-P(t))’
-P’(t)=at
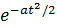
Приемник к началу наблюдения за отказами проработал 458 часов. К концу наблюдения наработка составила 2783 часа. Всего зарегистрировано 5 отказов. Среднее время ремонта Определить среднюю наработку на отказ
Задача №1 Система состоит из n параллельно соединенных равнонадежных подсистем, вероятность безотказной работы каждой из которых
Определить потребную кратность резервирования, чтобы вероятность безотказной работы системы была не ниже P0=0.98 Решение Pобщ(t)=1-[1-Pi(t)]n при параллельном соединении 1-[1-Pi(t)]n=>0.98 1-[1-0.85]n=>0.98 1-0.15n=>0.98 0.02=>0.15n n=> n=>2.06 Задача №2 Определить вероятность того, что за времяt=150 ч произойдет 0,2 и 2 отказа, если Решение Pn(t)= a= P0(t)= P0(t)= P0(t)=
Задача №3 Пусть вероятность безотказной работы ВС за время t=1000 ч составляет Р(1000)=0.98. Составить прогноз вероятности безотказной работы этой же системы через 100000 ч работы без обслуживания по экспоненциальной модели и модели Вейбулла при α=0.5.
P(100000)=0.817 Задача №4 Найти вероятность пребывания стационарной системы
7
Решение
P1+P2+P3=1 P2=1-P1-P3
_ 5*P1-2*P3=0 5*P1+13*P3=5 -15*P3=-5 P3=0.33 5*P1-2/3=0 P1=0.13 P2=1-1/3-2/15=0.53 Исходные данные: имеется система из n элементов следующего вида Задача №1
Pi=0,3 Найти вероятность передачи информации через диодный мост Решение: P = P1∙P2+P3∙P4-P1∙P2∙P3∙P4 = 0,3∙0,3+0,3∙0,3-0,3∙0,3∙0,3∙0,3 = 0,1719
|
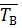составила 1,5 часа.
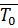и коэффициент готовности 
.
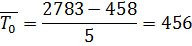
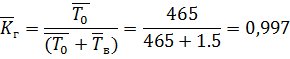
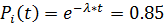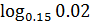
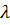=0.01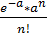
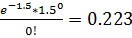
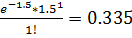
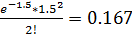
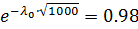
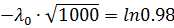
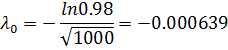
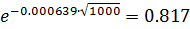
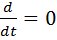в каждом из состояний
