Статистический смысл энтропии, формула Больцмана, термодинамическая вероятность состояния. Физический смысл закона неубывания энтропии.
Термодинамическая вероятность W состояния системы — это число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние (по определению, W³;1, т. е. термодинамическая вероятность не есть вероятность в математическом смысле (последняя £ 1!)).
Согласно Больцману (1872), энтропия системы и термодинамическая вероятность связаны между собой следующим образом:
где k — постоянная Больцмана. Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Формула Больцмана (57.8) позволяет дать энтропии следующее статистическое толкование: энтропия является мерой неупорядоченности системы. В самом деле, чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия. В состоянии равновесия — наиболее вероятного состояния системы — число микросостояний максимально, при этом максимальна и энтропия. Второй закон термодинамики – один из основных законов физики, закон о неубывания энтропии в изолированной системе.
2. Прирост энтропии в медленном квазистатического процессе равно
где T – температура. 16. Первое и второе начало термодинамики: формулировки и физический смысл. Существует несколько эквивалентных формулировок первого начала термодинамики В любой изолированной системе запас энергии остаётся постоянным. Это — формулировка Дж. П. Джоуля (1842 г.). Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, то есть, оно зависит только от начального и конечного состояния системы и не зависит от способа, которым осуществляется этот переход. Это определение особенно важно для химической термодинамики (ввиду сложности рассматриваемых процессов). Иными словами, внутренняя энергия является функцией состояния. В циклическом процессе внутренняя энергия не изменяется.
Изменение полной энергии системы в квазистатическом процессе равно количеству теплоты
Для элементарного количества теплоты
Разделение работы на две части, одна из которых описывает работу, совершённую над системой, а вторая — работу, совершённую самой системой, подчёркивает, что эти работы могут быть совершены силами разной природы вследствие разных источников сил. Важно заметить, что Существуют несколько эквивалентных формулировок второго начала термодинамики:
Эквивалентность этих формулировок легко показать. В самом деле, допустим, что постулат Клаузиуса неверен, то есть существует процесс, единственным результатом которого была бы передача тепла от более холодного тела к более горячему. Тогда возьмем два тела с различной температурой (нагреватель и холодильник) и проведем несколько циклов тепловой машины, забрав тепло С другой стороны, предположим, что неверен постулат Томсона. Тогда можно отнять часть тепла у более холодного тела и превратить в механическую работу. Эту работу можно превратить в тепло, например, с помощью трения, нагрев более горячее тело. Значит, из неверности постулата Томсона следует неверность постулата Клаузиуса. Таким образом, постулаты Клаузиуса и Томсона эквивалентны. Другая формулировка второго начала термодинамики основывается на понятии энтропии:
Такая формулировка основывается на представлении об энтропии как о функции состояния системы, что также должно быть постулировано. Второе начало термодинамики в аксиоматической формулировке Рудольфа Юлиуса Клаузиуса (R. J. Clausius, 1865) имеет следующий вид: Для любой квазиравновесной термодинамической системы существует однозначная функция термодинамического состояния В состоянии с максимальной энтропией макроскопические необратимые процессы (а процесс передачи тепла всегда является необратимым из-за постулата Клаузиуса) невозможны. 17. Учет размеров и взаимодействия молекул реального газа, константы a и b. Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса. 1. Учет собственного объема молекул. Наличие сил отталкивания, которые противодействуют проникновению в занятый молекулой объем других молекул, сводится к тому, что фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не V m, а V m — b, где b — объем,занимаемый самими молекулами. Объем b равен учетверенному собственному объему молекул. Если, например, в сосуде находятся две молекулы, то центр любой из них не может приблизиться к центру другой молекулы на расстояние, меньшее диаметра d молекулы. Это означает, что для центров обеих молекул оказывается недоступным сферический объем радиуса d, т. е. объем, равный восьми объемам молекулы или учетверенному объему молекулы в расчете на одну молекулу. 2. Учет притяжения молекул. Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением. По вычислениям Ван-дер-Ваальса, внутреннее давление обратно пропорционально квадрату молярного объема, т. е.
где а — постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения, V m — молярный объем. Вводя эти поправки, получим уравнение Ван-дер-Ваальса для моля газа (уравнение состояния реальных газов):
Для произвольного количества вещества v газа (v=m/M) с учетом того, что V=vV m, уравнение Ван-дер-Ваальса примет вид
где поправки а и b — постоянные для каждого газа величины, определяемые опытным путем (записываются уравнения Ван-дер-Ваальса для двух известных из опыта состояний газа и решаются относительно а и b). Эта изотерма называется критической, соответствующая ей температура T к — критической температурой; точка перегиба К называется критической точкой; в этой точке касательная к ней параллельна оси абсцисс. Соответствующие этой точке объем V к, и давление р к называются также критическими. Состояние с критическими параметрами (p к, V к, T к) называется критическим состоянием. При низких температурах (Т < T к) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь. Для пояснения характера изотерм преобразуем уравнение Ван-дер-Ваальса (61.2) к виду
Для нахождения критических параметров подставим их значения в уравнение (62.1) в запишем
(символ «m» для простоты опускаем). Поскольку в критической точке все три корня совпадают и равны V к уравнение приводится к виду
или
Tax как уравнения (62.2) и (62.3) тождественны, то в них должны быть равны и коэффициенты при неизвестных соответствующих степеней. Поэтому можно записать
Решая полученные уравнения, найдем
|

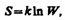 (57.8)
(57.8)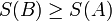 .
.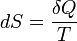 ,
,
 , сообщённому системе, в сумме с изменением энергии, связанной с количеством вещества
, сообщённому системе, в сумме с изменением энергии, связанной с количеством вещества  при химическом потенциале
при химическом потенциале  , и работы
, и работы 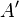 , совершённой над системой внешними силами и полями, за вычетом работы
, совершённой над системой внешними силами и полями, за вычетом работы 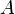 , совершённой самой системой против внешних сил
, совершённой самой системой против внешних сил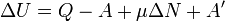 .
.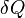 , элементарной работы
, элементарной работы 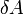 и малого приращения
и малого приращения 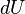 внутренней энергии первый закон термодинамики имеет вид:
внутренней энергии первый закон термодинамики имеет вид: .
. являются полными дифференциалами, а
являются полными дифференциалами, а 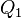 у нагревателя, отдав
у нагревателя, отдав 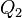 холодильнику и совершив при этом работу
холодильнику и совершив при этом работу  . После этого воспользуемся процессом Клаузиуса и вернем тепло
. После этого воспользуемся процессом Клаузиуса и вернем тепло  , называемая энтропией, такая, что ее полный дифференциал
, называемая энтропией, такая, что ее полный дифференциал  .
. (61.1)
(61.1) (61.2)
(61.2)
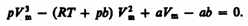 (62.1)
(62.1)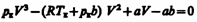 (62.2)
(62.2) (62.3)
(62.3)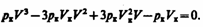
 (62.4)
(62.4)



