Z-ПРЕОБРАЗОВАНИЕ

 

Удобным средством изучения линейных разностных уравнений с начальными условиями и без них является дискретный аналог преобразования Лапласа или z-преобразование. Такое преобразование отображает полубесконечную последовательность дискретных значений на комплексную плоскость.

Определение Z - преобразования

Определив новую переменную

 

 

и подставив ее в уравнение преобразования Лапласа дискретной функции времени:

 

 

 

получаем z-преобразование импульсного сигнала х*(1):

 

 

Этот бесконечный ряд сходится, если все его члены |х(кТо)| ограничены и если справедливо условие |z|>l. Поскольку величина о может выбираться произвольно, сходимость имеет место для широкого класса функций х (кТо). Следует иметь в виду, что метод z- преобразования основывается на тех же предположениях, что и преобразование Лапласа, причем особенно важно выполнение условия х(кТ₀)=0 при к<0.

Ниже приведены некоторые важнейшие теоремы, используемые при вычислении z-преобразований.

а) Линейность

б) Сдвиг по времени вправо

в) Сдвиг по времени влево

 

г) Изменение масштаба по переменной z

д) Начальное значение

е) Конечное значение

 

ж) Свертка

 

Обратное z-преобразование

В отличие от преобразоваия Лапласа, для которого прямой и обратный переходы x(t)-»x(s) и x(s)-»x(t) выполняются однозначно, z- преобразование x(t)-»x(z) и обратное z-преобразование x(z)-»*x(t) не обладают этим свойством. Объясняется это тем, что они не учитывают поведения функции х (t) в промежутках между моментами срабатывания квантователя. В то же время преобразование x(kTo)-»x(z) и обратное преобразование x(z)-»x(kTo) взаимно однозначны.

На практике обратное z-преобразование вычисляют, записывая функцию x(z) как сумму элементарных членов, содержащихся в таблицах z-преобразований, или просто поделив числитель х (z) на ее знаменатель. В последнем случае получается ряд вида

 

x(z) = c₀+c₁-z'¹ + c₂-z'²+... (2.21)

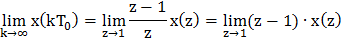
Из уравнения (2.21) следует, что 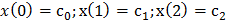и т.д.