Вывод волнового уравнения
Теперь можно перейти непосредственно к выводу волнового уравнения. Это можно сделать двумя способами.
Способ 1. Физические явления, происходящие в звуковой волне, обладают следующими тремя свойствами: 1. Газ движется, и плотность его меняется. 2. При изменении плотности меняется и давление. 3. Неравномерное распределение давления вызывает движение газа. Рассмотрим сначала свойство (2). Для любого газа, жидкости или твердого тела давление является функцией плотности. До прихода звуковой волны мы имели равновесное состояние с давлением Р 0 и плотностью ρ;0. Давление Р зависит от плотности среды Р = f (ρ;), и в частности равновесное давление Р 0 = f (ρ;0). Отклонения величины давления от равновесного в звуковой волне очень малы. Давление принято измерять в барах (1 бар = 105 н/м2). Давление в одну атмосферу приблизительно равно 1 бар (1 атм = 1,0133 бар). Для звука обычно используется логарифмическая шкала интенсивности, так как слуховое восприятие, грубо говоря, растет по логарифмическому закону. В этой децибельной шкале уровень звукового давления I связан с амплитудой звукового давления следующим образом:
где давление отнесено к некоторому стандартному давлению
котороесоответствует абсолютному порогу слышимости человеческого слуха. Звуковое давление Р = 103 Р отн = 2 Р = Р 0 + Р и, ρ = ρ;0 + ρ;и (3.2) можно считать, что изменение давления Р и очень мало по сравнению с Р 0, а изменение плотности ρ;и очень мало по сравнению с ρ;0. Тогда Р 0 + Р и = f (ρ;0 + ρ;и) = f (ρ;0) + ρ;и f ' (ρ;0), (3.3) где Р 0 = f (ρ;0) и f ' (ρ;0) – производная от f (ρ;0), взятая при значении ρ = ρ;0. Второе равенство здесь возможно только потому, что ρ;и очень мало. Таким образом, мы находим, что избыточное давление Р и пропорционально избыточной плотности ρ;и; коэффициент пропорциональности здесь можно обозначить через κ;: Р и = κρ;и, где κ; = f ' (ρ;0) = Это весьма простое соотношение и составляет точное содержание свойства (2). Перейдем теперь к свойству (1). Предположим, что положение элемента объема воздуха, не возмущенного звуковой волной, есть x, а звук смещает его в момент времени t на величину u (x, t), так что его новое положение есть x + u (x, t), как показано на рис. 3.1.
Далее, положение соседнего элемента объема есть x+ Δ x, и его смещенное положение есть x+ Δ x + u (x+ Δ x, t). Теперь можно найти изменение плотности. Поскольку мы рассматриваем плоскую волну, удобно взять единичную площадку, перпендикулярную оси x, т.е. направлению распространения волны. Количество воздуха, приходящееся на единичную площадку в интервале Δ x, есть ρ;0Δ x, где ρ;0 – невозмущенная, или равновесная, плотность воздуха. Эта порция воздуха, смещенная звуковой волной, будет находиться теперь между x + u (x, t)и x+ Δ x + u (x+ Δ x, t), причем количество воздуха в этом интервале то же самое, что и в интервале Δ x до прихода волны. Если через ρ; обозначить новую плотность, то ρ;0Δ x = ρ;[ x + Δ x + u (x+ Δ x, t) – x – u (x, t)] (3.5) Поскольку Δ x мало, можно написать u (x+ Δ x, t) – u (x, t) = (du / dx) Δ x. Здесь уже появляется частная производная, потому что u зависит и от x, и от времени. Наше уравнение принимает вид
или
Но в звуковой волне все изменения очень малы, так что ρ;и мало, u мало и du / dx тоже мало. Поэтому в уравнении, которое мы только что написали,
можно пренебречь
Именно такой вид уравнения можно было ожидать из чисто физических соображений. Если смещение различно для разных x, то плотность будет изменяться. Знак тоже правильный: если смещение u растет с ростом x, так что воздух расширяется, плотность должна уменьшаться. Теперь нам нужно найти третье уравнение – уравнение движения, производимого избытком давления. Зная соотношение между силой и давлением, можно получить уравнение движения. Возьмем объем воздуха толщиной Δ x и с единичной площадью грани, перпендикулярной x, тогда масса воздуха в этом объеме есть ρ;0Δ x, а ускорение воздуха есть d 2 u / dt 2, так что масса, умноженная на ускорение для этого слоя, есть ρ;0Δ x (d 2 u / dt 2). (Если Δ x мало, то безразлично, где брать ускорение – на краю слоя или где-нибудь посередине). Сила, действующая на единичную площадку нашего слоя, перпендикулярную оси x, должна быть равна ρ;0Δ x (d 2 u / dt 2). В точке x мы имеем силу P (x, t), действующую на единицу площади в направлении + x, а в точке x+ Δ x возникает сила, действующая в обратном направлении и по величине равная P (x+ Δ x, t) (рис. 3.2):
Мы здесь учли, что Δ x мало и что только избыточное давление Р и меняется в зависимости от x. Итак, в соответствии со свойством (3) мы получаем
Теперь уравнений уже достаточно, чтобы увязать все величины и привести к одной переменной, скажем x. Можно выразить Р и в (3.11) с помощью (3.4):
а затем исключить ρ;и с помощью (3.9). Тогда ρ;0 сократится и у нас останется
Обозначим
Это и есть волновое уравнение, которое описывает распространение звука в среде.
|

 (3.1)
(3.1) ,
, 10-7 бар соответствует довольно сильному звуку в 60 дБ. Таким образом, видно, что давление в звуковой волне меняется на очень малую величину в сравнении с равновесным или средним, равным 1 атм. Смещение и перепады плотности также очень малы. При взрывах, однако, изменения уже не столь малы; избыточное звуковое давление может превышать 1 атм. Такие большие перепады давления приводят к новым явлениям, которые мы рассмотрим позже. В звуковых волнах уровень силы звука выше 100 дБ встречается редко. Уровень силы звука в 120 дБ уже вызывает боль в ушах. Поэтому написав для звуковой волны
10-7 бар соответствует довольно сильному звуку в 60 дБ. Таким образом, видно, что давление в звуковой волне меняется на очень малую величину в сравнении с равновесным или средним, равным 1 атм. Смещение и перепады плотности также очень малы. При взрывах, однако, изменения уже не столь малы; избыточное звуковое давление может превышать 1 атм. Такие большие перепады давления приводят к новым явлениям, которые мы рассмотрим позже. В звуковых волнах уровень силы звука выше 100 дБ встречается редко. Уровень силы звука в 120 дБ уже вызывает боль в ушах. Поэтому написав для звуковой волны . (3.4)
. (3.4)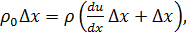 (3.6)
(3.6) (3.7)
(3.7) (3.8)
(3.8) (du / dx) по сравнению с
(du / dx) по сравнению с  (du / dx). Так мы приходим к соотношению, которое требовалось согласно свойству (1):
(du / dx). Так мы приходим к соотношению, которое требовалось согласно свойству (1): . (3.9)
. (3.9) (3.10)
(3.10)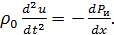 (3.11)
(3.11) , (3.12)
, (3.12) (3.13)
(3.13) тогда можно написать
тогда можно написать (3.14)
(3.14)


