Значения модуля Юнга для некоторых материалов
Обратимся вновь к элементарному цилиндрическому объему, изображенному на рис. 4.1, и напишем для него уравнение движения. До начала деформации левая поверхность (основание) этого объема располагается в точке с координатой х. При прохождении волны его точки сместятся в положение с координатой u, а правая поверхность (основание), имевшая до начала деформации координату х +Δ х, окажется в положении х +Δ х + u +Δ u. Полагая Δ х очень малой величиной, проекцию ускорения, которое получает элементарный цилиндр, на ось 0х можно считать для всех точек цилиндра одинаковой и равной d 2 u / dt 2. Масса цилиндра равна ρS Δ х, где ρ – плотность недеформированной среды. Проекция на ось 0х силы, действующей на цилиндр, равна произведению площади основания на разность нормальных напряжений в сечениях (х +Δ х + u +Δ u) и (x + u):
Значение производной du / dx в сечении x + δ; для δ; малых можно представить с большой степенью точности в виде ряда Тейлора для производной du / dx, вычисленной в точке х и оборванной на втором члене:
Подставим это выражение в (4.2), полагая δ; равным в одном случае u, а в другом случае Δ х + u +Δ u:
Учтем, что в этом выражении величины Δ х, u и Δ u являются малыми и оставим главный по значению член:
Относительное удлинение du / dx при упругих деформациях бывает много меньше единицы, поэтому du << dx, так что слагаемым Δ u в сумме Δ х +Δ u можно пренебречь. Подставив найденные значения массы, ускорения и силы в уравнение второго закона Ньютона (сила равна массе умноженной на ускорение: F = ma), получим:
откуда после деления на ES Δ х придем к уравнению:
которое представляет собой волновое уравнение. Сопоставление уравнений (4.5) и (3.21) показывает, что
Таким образом, фазовая скорость упругих продольных волн равна корню квадратному из модуля Юнга, деленного на плотность ρ; (подтверждение сформулированных ранее основополагающих свойств, которыми должна обладать среда, чтобы в ней распространялась волна – упругость и инертность). Приведем без вывода формулу для скорости распространения поперечных волн в твердых телах:
где G – модуль сдвига вещества твердого тела.
|

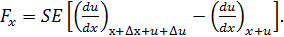 (4.2)
(4.2) . (4.3)
. (4.3)
 (4.4)
(4.4)
 (4.5)
(4.5) . (4.6)
. (4.6) , (4.7)
, (4.7)


