Способ 2
Уравнение любой волны является решением дифференциального уравнения, которое называется волновым. Чтобы установить вид волнового уравнения, определим вторые частные производные по координате х и времени t от функции Первая производная функции u по времени t будет выглядеть следующим образом:
а вторая производная
Первая производная функции u по координате x будет выглядеть следующим образом:
а вторая производная
Теперь в выражениях для вторых производных перенесем ω;2 и k 2 в левые части (разделив обе части на ω;2 и k 2 соответственно). Получим:
Следовательно,
или
Поскольку k = 2π/ λ;, ω; = 2π ν; = 2π с / λ;,то
Получаем:
или
Это так же, как и (3.14), есть дифференциальное уравнение плоской волны, распространяющейся вдоль оси 0 х. Оно получено нами из уравнения плоской волны (2.9) (см. лекцию 1). С помощью аналогичных рассуждений его можно получить и для плоской волны, бегущей в отрицательном направлении оси 0 х. Однако можно сделать и обратное заключение: если какая-нибудь физическая величина (не обязательно смещение u) зависит от времени t и координаты x так, что ее частные производные удовлетворяют уравнению (3.15), то эта величина распространяется в среде в виде плоской волны со скоростью с.
|

 , описывающей плоскую волну, распространяющуюся вдоль положительного направления оси 0х (плоская прогрессивная волна).
, описывающей плоскую волну, распространяющуюся вдоль положительного направления оси 0х (плоская прогрессивная волна). ,
, .
.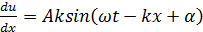 ,
, .
. и
и  .
.



 (3.15)
(3.15)


