КОЛЕБАНИЯ МАТЕМАТИЧЕСКОГО МАЯТНИКАКОЛЕБАНИЯ МАТЕМАТИЧЕСКОГО МАЯТНИКА
Колебательное движение – одно из самых распространенных в природе. Объект движется таким образом, что многократно проходит через одни и те же точки, периодически воспроизводя одно и то же состояние. Изучив его движение на сравнительно коротком отрезке времени, включающем один период, мы можем составить полное представление о его движении в будущем (если оно не будет изменено вмешательством извне). Прибегая к компьютерному моделированию, можно продвинуться в изучении колебаний математического маятника и понять закономерности колебательного движения глубже. Рассмотрим идеализированную систему, состоящую из тела массы m, прикрепленного к нижнему концу жесткого «невесомого» стержня длиной l, верхний конец которого вращается без трения в точке подвеса. Если груз отклонить от положения равновесия на угол θ0 и отпустить, то «математический маятник» будет колебаться в вертикальной плоскости. Поскольку движение груза происходит по дуге окружности радиуса l, то его положение характеризуется в каждое мгновение углом θ;. Линейная скорость и ускорение равны
На груз действуют две силы: сила тяжести
Обычно в курсе физики ограничиваются исследованием малых колебаний. Если
Решение его элементарно:
где θ = θ0, v = v0, то
или, как часто записывают,
где φ – так называемая, начальная фаза; А – амплитуда колебания; А и φ; легко выразить через начальные условия θ0 и v0:
Движение, происходящее по закону (1.25), называют гармоническим колебательным движением. Слово «гармонический» связывают с простотой тригонометрической функцией (синусом или косинусом); так, гармоническим является и движение Для изучения колебаний с большой амплитудой следует обратиться к уравнению (1.24), которое заведомо не интегрируется в элементарных функциях. Обезразмерим его, взяв за характерный масштаб времени период малого колебания. Если τ =t/Т, то
Это уравнение вообще не содержит параметров. Достаточно его решить, и мы составим полное представление о природе «больших» колебаний. В этом проявляется сила приема обезразмеривания. Сведем (1.26) к системе двух уравнений первого порядка:
Существенно, что система консервативна, и полная энергия сохраняется (до тех пор, пока мы не учитываем трение и воздействие извне).
В безразмерных переменных х и θ
Как и при моделировании движения небесных тел, сохранение Реальный период зависит от амплитуды колебания вопреки тому, что предсказывает теория, основанная на приближении малых колебаний. Широчайшее распространение в математике и ее приложениях, связанных с периодическими функциями, имеет, так называемый, гармонический анализ. Поскольку тригонометрические функции, соответствующие гармоническому движению, хорошо изучены и привычны, то стремление передать периодическое (но не гармоническое) движение хотя бы суммой нескольких гармонических вполне понятно. Все эти «гармоники» должны иметь, естественно, тот же период, что и изучаемая функция. Если ее период Т, то, кроме тригонометрических функций
причем число гармоник-слагаемых формально бесконечно велико. Если ограничится лишь небольшим числом гармоник, скажем, тремя, то коэффициенты можно приближенно найти интерполяцией. Взяв за узлы точки t = 0; 0.4; и 1 и решив систему трех линейных алгебраических уравнений, получим
Колебания маятника при наличии трения. Поскольку сила трения при малых скоростях пропорциональна скорости, а скорость
Преобразуем его к виду
где, как и выше,
Его решение таково: затухающие колебания при
при
Что же касается уравнения (1.31), то его аналитическое решение отсутствует, и при численном моделировании можно поставить ряд задач о том, насколько решения уравнений (1.20) и (1.31) различаются в зависимости от начальной амплитуды.
Вынужденные колебания. Если на маятник воздействует внешняя сила F(t), меняющаяся со временем, то уравнения движения получаются из (1.30) добавлением F(t) к правой части. Рассмотрим лишь случай периодического внешнего воздействия:
где
Движение, описываемое уравнением (1.33), состоит из двух этапов. На первом оно складывается из двух колебательных движений: затухающих собственных колебаний с частотой
А и В – произвольные постоянные, находятся из начальных условий. Исследования переходного процесса установления стационарных вынужденных колебаний, резонанса, биений, возникающих при к = 0 и Возвратимся к уравнению нелинейных вынужденных колебаний (1.32). Его аналитическое решение отсутствует, и возможно лишь численное. Сформулируем ряд задач: как нелинейность влияет (при больших амплитудах движения) на период вынужденных колебаний, на резонанс, на период биений при
Параметрические колебания. Рассмотрим еще один вид колебаний маятника, когда на него внешние силы непосредственно не действуют, но внутри системы происходят некоторые события, приводящие к зависимости от времени параметров, входящих в уравнение движения. В этом случае колебательные движения называют параметрическими. Простейший пример – раскачивание качелей усилиями того человека, который стоит на этих качелях. Все знают, что, приседая и отталкиваясь «в такт», можно сильно разогнать качели. Указанные приседания сводятся к периодическому изменению центра тяжести системы, или, что почти равносильно, длины нити подвеса. Поскольку длина нити подвеса определяет частоту колебаний, то математическая модель явления – уравнение
где
где λ – частота изменения величины При малых амплитудах колебаний и отсутствии трения уравнение (1.35) превращается в
Решение любого из этих уравнений возможно лишь численно. Одна из особенностей уравнения (1.36) – так называемый, параметрический резонанс – допускает частичное аналитическое исследование, однако слишком сложное, чтобы его здесь проводить. Параметрический резонанс состоит в том, что при некоторых соотношениях частот λ; и Как можно численно установить границу зоны параметрического резонанса, например, первой? – Для этого следует задаться некоторыми значениями α (например 0.1) и γ (например 0.3), не принадлежащими зоне неустойчивости, и проинтегрировать численно уравнение (1.36). Удобно предварительно обезразмерить время переменной
Здесь Нарастание колебаний при параметрическом резонансе, описываемом уравнением (1.37), является неограниченным. Физически такого быть не может. Ограничение амплитуды колебаний наступает либо за счет учета трения, либо при возврате к sinθ; в уравнении (1.35), либо за счет обоих факторов. Следует учесть, что наличие трения не только ограничивает размах параметрических колебаний, но и «приподнимает» зоны параметрического резонанса над осью γ на фазовой плоскости α, γ, причем в разной мере. Моделирование этого и других явлений при параметрическом резонансе – интересная исследовательская работа.[2]
Многогранность задачи об одномерных колебаниях. Колебания математического маятника одномерны в том смысле, что они описываются одной функцией Оказывается, что рассмотренные выше уравнения, особенно линейные (т.е. малых колебаний), обладают высокой универсальностью и описывают ряд процессов в механике твердых тел, газов, в электродинамике и т.д. Так, уравнение малых колебаний
описывает указанные ниже и другие системы (при этом в х, к, · математический маятник; · пружинный маятник, где сила, действующая на тело, определяется законом Гука; · «физический» маятник – тело, свободно вращающееся около горизонтальной оси; · крутильный маятник наручных часов – симметричное тело, совершающее колебания около вертикальной оси под действием спиральной пружины; · ток в колебательном контуре; · акустический резонатор Гельмгольца, в котором происходят колебания воздуха в колбе с широким горлышком; · колебания магнитной стрелки компаса. Таким образом, наше внимание к колебательному движению не является преувеличенным.
|

 (1.23)
(1.23) и упругая сила натяжения стержня
и упругая сила натяжения стержня  . При выводе уравнения движения достаточно учесть лишь компоненту силы
. При выводе уравнения движения достаточно учесть лишь компоненту силы  , направленную по касательной к дуге, то есть ее величина равна
, направленную по касательной к дуге, то есть ее величина равна 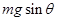 , а направлена она в сторону уменьшения θ, поэтому:
, а направлена она в сторону уменьшения θ, поэтому: 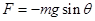 . Силу F называют возвращающей силой. Сила
. Силу F называют возвращающей силой. Сила 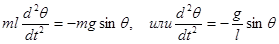 (1.24)
(1.24)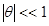 , то уравнение (1.24) можно считать эквивалентным (так как
, то уравнение (1.24) можно считать эквивалентным (так как 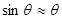 ; здесь и далее используется радианная мера углов) уравнению
; здесь и далее используется радианная мера углов) уравнению
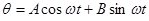
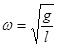 -- собственная частота,
-- собственная частота, 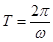 -- период колебания маятника. Значения А и В зависят от начальных условий. Если при t = 0
-- период колебания маятника. Значения А и В зависят от начальных условий. Если при t = 0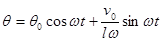
 (1.25)
(1.25)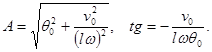
 к которому можно свести (1.25).
к которому можно свести (1.25).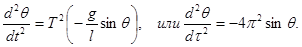 (1.26)
(1.26) (1.27)
(1.27) (1.28)
(1.28) (1.29)
(1.29) в ходе интегрирования – прекрасный критерий для изучения устойчивости метода, выбора шага и т.д.
в ходе интегрирования – прекрасный критерий для изучения устойчивости метода, выбора шага и т.д.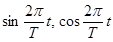 период Т имеют и функции с частотами, кратными
период Т имеют и функции с частотами, кратными  т.е.
т.е. 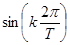 ,
,  при любом целом к > 0. Гармоническое разложение функции f(t) с периодом Т в общем случае имеет вид
при любом целом к > 0. Гармоническое разложение функции f(t) с периодом Т в общем случае имеет вид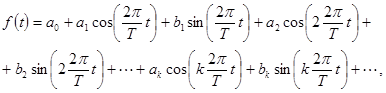

 .
.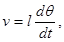 то уравнение свободных колебаний маятника с учетом трения выглядит так:
то уравнение свободных колебаний маятника с учетом трения выглядит так: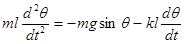
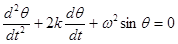 (1.30)
(1.30)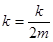 . При малых колебаниях уравнение (1.30) превращается в
. При малых колебаниях уравнение (1.30) превращается в (1.31)
(1.31) и затухание без колебаний при
и затухание без колебаний при  . Все это возможно проверить в ходе численного моделирования, хотя уравнение (1.31) допускает аналитическое решение. Приведем его: при
. Все это возможно проверить в ходе численного моделирования, хотя уравнение (1.31) допускает аналитическое решение. Приведем его: при 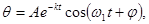
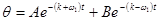
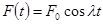 , где λ; – частота вынуждающей силы. Имеем уравнение движения маятника:
, где λ; – частота вынуждающей силы. Имеем уравнение движения маятника: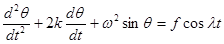 (1.32)
(1.32) . При малой амплитуде результирующего движения уравнение (1.33) примет вид
. При малой амплитуде результирующего движения уравнение (1.33) примет вид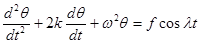 (1.33)
(1.33) (при
(при  1 и резко возрастает при
1 и резко возрастает при 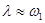 -- явление резонанса, описанное в любом учебнике физики. Численное интегрирование уравнения (1.33) необязательно, так как решение можно записать в виде формул, содержащих лишь элементарные функции:
-- явление резонанса, описанное в любом учебнике физики. Численное интегрирование уравнения (1.33) необязательно, так как решение можно записать в виде формул, содержащих лишь элементарные функции: (1.34)
(1.34)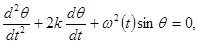
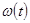 -- заданная функция, определяющая закон изменения частоты. Мы ограничимся простейшим случаем гармонического изменения
-- заданная функция, определяющая закон изменения частоты. Мы ограничимся простейшим случаем гармонического изменения 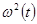 :
: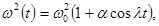
 (1.36)
(1.36) , а именно
, а именно 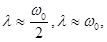
 и при определенных значениях величины α в системе возникают нарастающие колебания.
и при определенных значениях величины α в системе возникают нарастающие колебания. , после чего уравнение примет вид
, после чего уравнение примет вид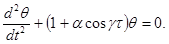 (1.37)
(1.37) . Затем, медленно учитывая γ (например, с шагом 0.01) и не меняя α, интегрировать уравнение (1.37), пока не попадешь в зону неустойчивости, и далее, пака не выйдешь из нее. Затем следует увеличить α (например, взяв α = 0.2) и снова повторить процедуру прохождения по значениям γ и т.д. – постепенно вырисуется картина границы зоны параметрического резонанса на фазовой плоскости.
. Затем, медленно учитывая γ (например, с шагом 0.01) и не меняя α, интегрировать уравнение (1.37), пока не попадешь в зону неустойчивости, и далее, пака не выйдешь из нее. Затем следует увеличить α (например, взяв α = 0.2) и снова повторить процедуру прохождения по значениям γ и т.д. – постепенно вырисуется картина границы зоны параметрического резонанса на фазовой плоскости.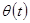 (хотя они и происходят в двумерном пространстве – плоскости, но жесткий стержень ликвидирует одну из степеней свободы, и в обычных декартовых координатах выражаются друг через друга).
(хотя они и происходят в двумерном пространстве – плоскости, но жесткий стержень ликвидирует одну из степеней свободы, и в обычных декартовых координатах выражаются друг через друга).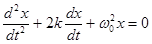 (1.2)
(1.2)


