А. Энтропия источника независимых сообщений
Количество информации в отдельном сообщении оценить достаточно просто. Следующей задачей является исследование информационных свойств источника сообщений в целом – например, определение среднего количества информации, приходящегося на одно сообщение. Для равновероятных сообщений количество информации в каждом из них определяется формулой (5.6). Среднее количество информации также равно Однако в реальных условиях сообщения имеют разную вероятность, например некоторые буквы алфавита встречаются в тексте гораздо чаще, чем другие. Поэтому требуется, кроме числа сообщений Среднее количество информации, приходящееся на одно сообщение (математическое ожидание)
В физике энтропия определяет степень неопределенности состояния системы. В теории информации энтропия имеет сходный смысл и характеризует неопределенность ситуации до передачи сообщения (т.к. оно заранее неизвестно). Чем выше уровень неопределенности, тем большуюинформацию в среднем несет одно сообщение источника Пример. Энтропия источника, генерирующего лишь два сообщения
Рис. 5.1. Зависимость энтропии двоичного источника от вероятности Энтропия данного источника максимальна при равных вероятностях генерации сообщений ( Основные свойства энтропии источника независимых сообщений: Ø Энтропия всегда положительна, что следует из неравенства Ø При равновероятных сообщениях
энтропия максимальна и равна
Ø Энтропия принимает нулевое значение лишь тогда, когда вероятности генерации всех сообщений ансамбля, кроме одного, равны нулю; Ø Энтропия независимых источников обладает свойством аддитивности, т.е. энтропия совокупности нескуольких источников равна сумме энтропий этих источников
|

 , и информационные свойства источника зависят только от числа сообщений
, и информационные свойства источника зависят только от числа сообщений  в ансамбле.
в ансамбле. , каждое из которых несет различное количество информации в соответствии с формулой
, каждое из которых несет различное количество информации в соответствии с формулой 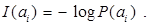
 :
: называется энтропией.
называется энтропией. и
и  с вероятностями
с вероятностями  , равна (см. Рис. 5.1)
, равна (см. Рис. 5.1)

 ), что соответствует наиболее неопределенной ситуации. Напротив, при
), что соответствует наиболее неопределенной ситуации. Напротив, при  или
или  , неопределенность отсутствует
, неопределенность отсутствует  ;
;





