Измеряемые параметры напряжения (тока)
Измерение токов и напряжений
В технике связи напряжения измеряют значительно чаще, чем токи. При измерении этих величин есть ряд общих закономерностей. Поэтому дальше, рассматривая измерения напряжений, будет отмечаться то, что справедливо и для токов.
Если измеряется постоянное во времени напряжение, то результат измерения – численное значение - отождествляется с величиной этого напряжения. Если же напряжение (ток) изменяется во времени, а результат измерения выражен числом, то на первый взгляд непонятно, как это число связано с изменяющейся измеряемой величиной.
U( U( Рис.8.1
Как показано на рис.8.1, значения текущего напряжения в моменты времени Как же результат измерения связан с изменяющимся во времени напряжением? Считается, что измерить переменное напряжение (ток) – означает измерить интегральный параметр текущего напряжения. Установлено четыре таких интегральных параметра (используются обычно три последних): 1) Среднее значение:
2) Средневыпрямленное значение:
3) Среднеквадратическое значение:
4) Максимальное (пиковое) значение Интегрирование при определении параметров проводится за время Связь между рассмотренными параметрами описывается тремя коэффициентами: коэффициентом амплитуды (пик-фактор) По определению
Кроме того, 1
Для сигнала пилообразной формы (u(t)=
Для прямоугольных однополярных импульсов со скважностью
На какой параметр реагирует вольтметр, зависит от типа детектора (преобразователя). Если говорить о стрелочном вольтметре, то «реагирует» означает, что стрелка индикатора прибора повернется на угол, пропорциональный параметру, соответствующему типу детектора (если детектор пиковый, то пропорционально Если рассмотреть вольтметр (амперметр) непосредственной оценки (существуют различные другие типы, например, компенсационный), то его модель, удобная для рассмотрения вопросов, связанных с градуировкой, может быть представлена в виде рисунке 8.2. На рисунке обозначено: U(t) – сигнал, подлежащий измерению; a - отклик преобразователя (отклонение стрелки), пропорциональный одному из параметров. Это зависит от вида преобразователя;
U(t) a
Рис.8.2
Из-за того, что у вольтметров используются детекторы трёх типов, важным является то, как они проградуированы. Эти два фактора определяют так называемую зависимость показаний вольтметра от формы измеряемого напряжения. Рассмотрим процесс градуировки, чтобы понять в чём заключается эта зависимость. Не останавливаясь на специфических особенностях процесса градуировки, можно рассмотреть этот процесс с помощью следующей схемы рисунке 8.3.
Рис.5.3
На схеме индекс «1» относится к пиковому вольтметру, «2»- средневыпрямленному, «3»- квадратичному. Меняя амплитуду сигнала на выходе генератора, будем снимать показание образцового вольтметра и «переносить» его на шкалы градуируемых в то место, которое указали стрелки (т.е. в соответствии с углом поворота a). Так как у градуируемых вольтметров преобразователи разные, то на один и тот же сигнал генератора при одном и том же показании образцового вольтметра у градуируемых вольтметров отклонения a будут разными, то есть градуировочные характеристики вольтметров с разными преобразователями будут различны. Принято вольтметры переменного напряжения градуировать на синусоидальном сигнале в среднеквадратических значениях – именно поэтому в рассматриваемой схеме генератор синусоидального сигнала, а образцовый вольтметр показывает среднеквадратичное значение. В некоторых случаях градуируют и в других значениях синусоидального напряжения – например, пиковый вольтметр градуируют в амплитудных значениях, но тогда это специально оговаривается. При входном синусоидальном сигнале после проведенной таким образом градуировке, показания всех вольтметров будут среднеквадратическим значением, то есть для синусоидального сигнала можно записать следующие зависимости:
где
В соответствии с (8.8) и (8.9) можно записать:
Выражения (8.10) отображают структуру показаний вольтметров с разными детекторами, при условии что они проградуированы в среднеквадратических значениях синусоидального напряжения. Как видно, в показаниях присутствуют градуировочные коэффициенты, выраженные через коэффициенты амплитуды и формы синусоидального напряжения. Теперь тремя вольтметрами, проградуированными в среднеквадратических значениях синусоидального напряжения, измерим напряжение произвольной формы
Из (8.11) видно, что только показание третьего вольтметра Из всего сказанного можно сделать вывод: если вольтметр проградуирован в значениях параметра, на который реагирует его преобразователь, то показание вольтметра при любой форме измеряемого сигнала равно параметру этого сигнала. В этом случае показания вольтметра не зависят от формы измеряемого напряжения. Это, например, справедливо для пикового вольтметра, проградуированного в пиковых значениях синусоидального сигнала. Оценим систематическую погрешность, возникающую из-за влияния формы сигнала. По показанию первого можно определить пиковое значение измеряемого несинусоидального сигнала
Зная
Рассуждая аналогично, для вольтметра средневыпрямленных значений:
Из полученных выражений для погрешностей можно сделать вывод, что пренебрежение влиянием формы измеряемого напряжения вызывает тем большую погрешность, чем больше измеряемое напряжение Вольтметр, как и другие измерительные приборы, может быть с открытым или закрытым входом. Напомним, что при открытом входе измеряется весь сигнал, а при закрытом измеряется сигнал без постоянной составляющей. Значение градуировочного коэффициента вольтметра не изменится, если с открытого входа перейти на закрытый (и наоборот), так как у синусоидального сигнала, на котором осуществлялась градуировка, постоянная составляющая равна нулю. В общем виде можно записать: СF[u(t)] при открытом входе;
СF[u(t) - где
8.2 Обобщенная структура вольтметра Обобщенная структурная схема аналогового вольтметра, показанная на рисунке 8.4, включает все возможные блоки. Здесь u(t) – измеряемый сигнал, Ап - показание, снимаемое со шкалы
Рис. 8.4.
В зависимости от назначения и характеристик вольтметра некоторые из блоков в конкретном вольтметре могут отсутствовать, за исключением электромеханического преобразователя (т.е. в просторечии стрелочного прибора, индикатора), который и без других блоков является простейшим аналоговым вольтметром.
Исходный динамический диапазон изображенного на рис 8.4. вольтметра соответствует динамическому диапазону электромеханического преобразователя. Для расширения диапазона в сторону больших измеряемых напряжений во входном устройстве устанавливается ступенчатый аттенюатор с точно известными коэффициентами деления каждой ступени; для расширения в сторону меньших – сигнал усиливается (при этом коэффициент усиления должен быть известен).
Быстродействие вольтметра лимитируется быстродействием самого инерционного блока – электромеханического преобразователя и не может быть увеличено дополнительными блоками. Включение дополнительных блоков не только расширяет динамический диапазон, но и увеличивает чувствительность, расширяет его возможности. Например, если усилитель обеспечивает частотную избирательность, то получается селективный вольтметр.
В стробоскопических цифровых вольтметрах, структура которого во многом подобна структуре цифрового осциллографа, и в так называемых виртуальных измерительных приборах проблемы влияния показания от формы можно избежать. В таких приборах входной сигнал с высокой скоростью дискретизируется и квантуется, как показано на рисунке 5.6.
U(t)
t Рис.5.6. В результате непрерывный сигнал заменяется массивом чисел, представляющих мгновенные значения сигнала в дискретные моменты времени
Например: Среднеквадратическое значение:
Средневыпрямленное значение:
|



 )
) t
t .
.

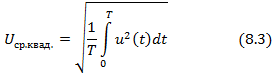
 ; (8.4)
; (8.4)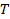 , которое равно времени одного измерения. В пос леднем выражении операция
, которое равно времени одного измерения. В пос леднем выражении операция  означает, что на интервале от 0 до Т (т.е. за время измерения) выбирается наибольшее значение (на рисунке 8.1 ему соответствует U(
означает, что на интервале от 0 до Т (т.е. за время измерения) выбирается наибольшее значение (на рисунке 8.1 ему соответствует U( , коэффициентом формы
, коэффициентом формы  , коэффициентом усреднения
, коэффициентом усреднения  .
. ;
; 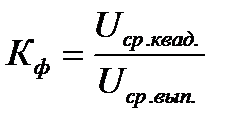 ;
;  (8.5)
(8.5) ; знак равенства выполняется для постоянного напряжения, сигналов типа «меандр». Для каждой формы физически реализуемого сигнала все три коэффициента определены, и их значения не зависят от параметров сигнала (таких как амплитуда, фаза, частота – важна только форма). Так для синусоидального сигнала
; знак равенства выполняется для постоянного напряжения, сигналов типа «меандр». Для каждой формы физически реализуемого сигнала все три коэффициента определены, и их значения не зависят от параметров сигнала (таких как амплитуда, фаза, частота – важна только форма). Так для синусоидального сигнала
 ;
; 
 ;
; 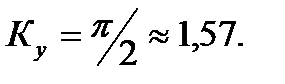 (8.6)
(8.6) ; 0
; 0  t£ Т):
t£ Т): ;
;  ;
;  . (8.7)
. (8.7) :
:
 (
( , где Т –период, t - длительность импульса)
, где Т –период, t - длительность импульса) , если квадратичный, то
, если квадратичный, то  ). Стрелка проектируется на шкалу, которая должна быть проградуирована в значении какого-либо параметра, но в зависимости от значения параметра показание будет различным.
). Стрелка проектируется на шкалу, которая должна быть проградуирована в значении какого-либо параметра, но в зависимости от значения параметра показание будет различным. - показание, снятое с отсчетного устройства.
- показание, снятое с отсчетного устройства.





 ;
;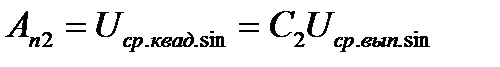 ; (8.8)
; (8.8) ,
,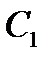 ,
,  ,
,  - градуировочные коэффициенты соответствующих вольтметров. Используя выражения (8.8), формально выразим их через коэффициенты амплитуды и формы:
- градуировочные коэффициенты соответствующих вольтметров. Используя выражения (8.8), формально выразим их через коэффициенты амплитуды и формы:
 (8.9)
(8.9)

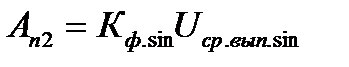 (8.10)
(8.10)
 Каждый преобразователь в соответствии со своей характеристикой преобразования сформирует отклик, пропорциональный размеру интегрального параметра напряжения
Каждый преобразователь в соответствии со своей характеристикой преобразования сформирует отклик, пропорциональный размеру интегрального параметра напряжения  ;
;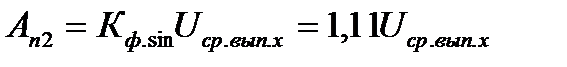 ; (8.11)
; (8.11)
 при измерении
при измерении 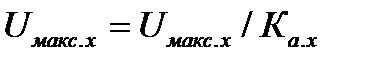 и
и  , следовательно,
, следовательно,  .
. .
. и
и 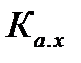 , можно найти среднеквадратическое значение измеряемого напряжения
, можно найти среднеквадратическое значение измеряемого напряжения  . Если пренебречь влиянием формы измеряемого напряжения, то есть принять показание
. Если пренебречь влиянием формы измеряемого напряжения, то есть принять показание  .
. 
 .
.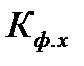 ) от соответствующих коэффициентов синусоидального напряжения (
) от соответствующих коэффициентов синусоидального напряжения ( и
и  ).
).
 ] при закрытом входе
] при закрытом входе - постоянная составляющая измеряемого сигнала, равная среднему значению.
- постоянная составляющая измеряемого сигнала, равная среднему значению.

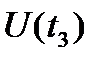

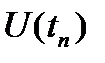
 (5.13)
(5.13) (5.14)
(5.14)


