Редактор Н.Е. Гладких
Рис 1. Вагинальное исследование у коровы № 6018.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
Утверждено на заседании кафедры физики 08 февраля 2012 г.
Методические указания к практическим занятиям «Молекулярная физика и термодинамика»
для всех специальностей и для всех профилей всех направлений бакалавриата очной и заочной форм обучения
Ростов-на-Дону
УДК 531.383 Методические указания к практическим занятиям «Молекулярная физика и термодинамика». – Ростов н/Д: Рост. гос. строит. ун-т, 2012. – 8 с.
Содержится краткая теория по молекулярной физике и термодинамике, в качестве пояснений к решению серии задач данного раздела физики. Основаны на учебном пособии «Курс физики» и на «Сборнике задач по курсу физики» Т.И. Трофимовой (изд-во «Высшая школа»), соответствующих действующей программе курса физики. Предназначены для проведения практического занятия «Молекулярная физика и термодинамика» по программе курса физики для студентов всех специальностей и профилей всех направлений бакалавриата очной и заочной форм обучения.
УДК 531.383 Составитель: профессор В.И. Снежков Рецензент: доцент Ю.И. Гольцов Редактор Н.Е. Гладких Темплан 2012 г., поз. ___ Подписано в печать 16.05.12. Формат 60х84 1/16. Ризограф. Бумага писчая. Уч.-изд.л 0,3. Тираж 25 экз. Заказ Редакционно-издательский центр Ростовского государственного строительного университета. 334022, Ростов-на-Дону, ул. Социалистическая, 162
© Ростовский государственный строительный университет, 2012
Краткая теория по теме: «Молекулярная физика и термодинамика» □ Идеальный газ – это такая модель газа, в которой не учитывают размеры молекул, их взаимодействие, а столкновение молекул рассматривают как абсолютно упругий удар. □ Основное уравнение молекулярно–кинетической теории газа устанавливает зависимость между давлением газа на стенки сосуда и средней кинетической энергией движения молекул: давление идеального газа зависит от концентрации молекул n и их средней кинетической энергии ‹eк› молекул: р = ⅔ n‹eк› = (2/3)n∙mv2/2; где концентрация n молекул – это отношение числа всех молекул к занимаемому ими объему V: n = N/V. □ Средняя квадратичная скорость молекул: ‹vкв› = m ― масса молекулы, M ―молярная масса газа. □ Среднее значение модуля скорости: ‹v› = □ Уравнение состояния газа (уравнение Менделеева-Клапейрона): pV = (m/M)RT Это уравнение можно преобразовать к виду: р = nkT □ Первое начало термодинамики: изменение внутренней энергии системы ΔU при каком-либо переходе из состояния 1 в состояние 2 равно разности переданного количества Q теплоты и работе A совершаемой системой: ΔU = Q – A или Q = ΔU + A □ Внутренняя энергия U идеального газа определяется только кинетической энергией хаотического движения его молекул: U = N‹eк› = N
Примеры решения задач по теме «Молекулярная физика и термодинамика» (Номера задач в скобках соответствуют сборнику задач по курсу физики Трофимовой Т.И.) Задача №1 (2.7). Азот массой 7 г находится под давлением р = 0,1 МПа и при температуре Т1 = 290 К. Вследствие изобарного нагревания азот занял объем V2 = 10 л. Определите: 1) объем (V1) газа до расширения; 2) температуру Т2 газа после расширения; 3) плотности газа до (ρ1) и после (ρ2) расширения.
Дано: М = 28∙103 кг/моль; m = 7 г = 7∙10-3 кг; р = 0,1 МПа = 0,1∙106 Па; Т1 = 290 К; V2 = 10 л = 10∙10-3 м3. V1 -? Т2 -? ρ1 -? ρ2 -? РЕШЕНИЕ Запишем уравнение Менделеева – Клапейрона до расширения газа и найдем объем V1: рV1 = (m/M)RT1; V1 = R- газовая постоянная; Т1 – температура до расширения. V1 = Запишем уравнение Менделеева -Клапейрона после расширения газа и найдем температуру Т2: рV2 = m/M)RT2; Т2 =
плотность газа до расширения: ρ1 = m/V1; ρ1 =
Ответ: 6,02∙10-3 м-3; 481 К; 1,16 кг/м3; 0,7 кг/м3. Задача №2 (2.15). Определите скорости молекул азота (N2) при 27 оС: 1) наиболее вероятную υв; 2) среднюю арифметическую ‹υ›; 3) среднюю квадратичную ‹υкв›.
Дано: М = 28∙103 кг/моль; t = 27 оС. υв -? ‹υ› -? ‹υкв›-? РЕШЕНИЕ 1) наиболее вероятная скорость молекул: υв = 2) средняя арифметическая скорость: ‹υ› = 3) средняя квадратичная скорость: ‹υкв› = Ответ: 422 м/с; 476 м/с; 517 м/с. Задача №3 (2.30). Определите среднюю длину свободного пробега ‹ℓ› молекул кислорода, находящегося при температуре 0 оС, если среднее число ‹z› столкновений, испытываемых молекулой в 1 с, равно 3,7∙109.
Дано: ‹z› = 3,7∙109 с-1; t = 0 oC. ‹ℓ› -?
РЕШЕНИЕ Средняя длина свободного пробега ‹ℓ› молекул за 1 с определяется как отношение средней арифметической скорости ‹υ› молекулы к числу
столкновений молекулы ‹z›: ‹ℓ› = ‹υ›/‹z›; ‹υ› = Ответ: 115∙10-9 м.
Задача №4 (2.54). Кислород массой 32 г находится в закрытом сосуде под давлением 0,1 МПа при температуре 290 К. После нагревания давление в сосуде повысилось в 4 раза. Определите: 1) объем сосуда; 2) температуру, до которой газ нагрели; 3) количество теплоты, сообщенное газу.
Дано: m = 32 г = 32∙10-3 кг; р1 = 0,1 МПа = 105 Па; T1 = 290 K; р2 = 4р1. V -? T2 -? Q -?
РЕШЕНИЕ 1) объем газа определим из уравнений Менделеева – Клапейрона: р1V = (m/M)RT1; V = 2) температуру газа Т2 после нагревания определим из закона Шарля: р1/Т1 = р2/Т2; Т2 = р2Т1/р1; Т2 = 4∙T1; T2 = 4∙290 = 1160 K. 3) количество теплоты, сообщенное газу: Q = CV∙(m/M)∙(T2 – T1); CV = iR/2 – молярная теплоемкость газа при постоянном объеме; i = 5 – число степеней свободы молекулы. Q = Ответ: 2,41∙10-2 м3; 1160 К; 18,1∙103 Дж. Задача №5 (2.58). Азот массой 280 г расширяется в результате изобарного процесса при давлении р = 1 МПа. Определите: 1) работу расширения; 2) конечный объем V2 газа, если на расширение затрачена теплота Q = 5 кДж, а начальная температура азота Т1 = 290 К.
Дано: М = 28∙10-3 кг/моль; m = 280 г = 0,28 кг; р = 1 МПа = 106 Па; Q = 5 кДж = 5∙103 Дж;; Т1 = 290 К. А -? V2 -? РЕШЕНИЕ 1) работа А при расширении газа и затраченная теплота Q при изобарном процессе определяются по формулам: A = (m/M)R(T2 – T1); Q = (m/M)Cp(T2 – T1). Разделим: A/Q = R/Cp; R – газовая постоянная; молярная теплоемкость при постоянном давлении: Ср = Подставим: А = V2 = (1/106)(1,43∙103 + Ответ: 1,43 Задача №6 (2.61). Азот массой 14 г сжимают изотермически при температуре Т = 300 К от давления р1 = 100 кПа до давления р2 = 500 кПа. Определите: 1) изменение внутренней энергии газа; 2) работу сжатия; 3) количество выделившейся теплоты.
Дано: М = 28∙10-3 кг/моль; m = 14 г = 0,014 кг; T = 300 K; р1= 100 кПа = 105 Па; р2 = 500 кПа =5∙105 Па. ΔU -? A -? Q -?
РЕШЕНИЕ Процесс изотермический, поэтому изменение внутренней энергии ΔU = 0. Работа при изотермическом процессе: А = (m/M)RT∙ℓn(p1/p2), т.е. A = (0.28/0.028)∙8,31∙300∙ℓn(105/5∙105) = -2,01∙103 Дж. Из первого начала термодинамики Q = ΔU + A видно, что количество выделившейся теплоты Q равно работе A сжатия: Q = A = 2,01∙103 Дж.
Ответ: 0; -2,01∙103 Дж; 2,01∙103 Дж.
|


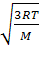 =
=  R = 8,31 Дж/(моль∙К) - универсальная (молярная) газовая постоянная; k = R/NA = 1,38∙10-23 Дж/К - постоянная Больцмана;
R = 8,31 Дж/(моль∙К) - универсальная (молярная) газовая постоянная; k = R/NA = 1,38∙10-23 Дж/К - постоянная Больцмана; . □ Наиболее вероятное значение модуля скорости: vв =
. □ Наиболее вероятное значение модуля скорости: vв = 
 kT =
kT =  RT, где i – число степеней свободы (для одноатомного газа равно 3, для двухатомного – 5).
RT, где i – число степеней свободы (для одноатомного газа равно 3, для двухатомного – 5).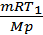 ; m – масса газа; М – молярная масса;
; m – масса газа; М – молярная масса; = 6,02∙10-3 м-3;
= 6,02∙10-3 м-3;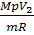 ; Т2 =
; Т2 = 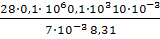 = 481 К;
= 481 К; = 1,16 кг/м3; плотность газа после расширения: ρ2 = m/V2; ρ2 =
= 1,16 кг/м3; плотность газа после расширения: ρ2 = m/V2; ρ2 =  = 0,7 кг/м3.
= 0,7 кг/м3. ; R – газовая постоянная; Т – абсолютная температура: Т = 273 + 27 = 300 К. М – молярная масса. υв =
; R – газовая постоянная; Т – абсолютная температура: Т = 273 + 27 = 300 К. М – молярная масса. υв =  = 422 м/с.
= 422 м/с. ; ‹υ› =
; ‹υ› =  = 476 м/с.
= 476 м/с. ; ‹υкв› =
; ‹υкв› =  = 517 м/с.
= 517 м/с. ∙
∙  ; ‹ℓ› =
; ‹ℓ› =  ∙
∙  = 115∙10-9 м.
= 115∙10-9 м. ; V =
; V =  = 2,41∙10-2 м3. М – молярная масса кислорода; R− газовая постоянная; Т1 – начальная температура; р1 – начальное давление.
= 2,41∙10-2 м3. М – молярная масса кислорода; R− газовая постоянная; Т1 – начальная температура; р1 – начальное давление. R(T2 – T1) = Q = 3
R(T2 – T1) = Q = 3  = 18,1∙103 Дж.
= 18,1∙103 Дж. ; i = 5 – число степеней свободы молекулы.
; i = 5 – число степеней свободы молекулы. =
= 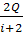 ; А =
; А =  = 1,43
= 1,43  3 Дж. 2) из уравнения Менделеева -Клапейрона определим объем V1 до расширения азота: рV1 = (m/M)RT1; V1 =
3 Дж. 2) из уравнения Менделеева -Клапейрона определим объем V1 до расширения азота: рV1 = (m/M)RT1; V1 =  RT1; подставим объем V1 в формулу работы газа и найдем конечный объем V2. A = p(V2 – V1); V2 = A/p + V1 = (1/p)(A + mRT1/M);
RT1; подставим объем V1 в формулу работы газа и найдем конечный объем V2. A = p(V2 – V1); V2 = A/p + V1 = (1/p)(A + mRT1/M); ) = 0,026 м3.
) = 0,026 м3.


