Задание 4. Формула называется выполнимой, если существует такой набор высказываний, который обращает эту формулу в истинное высказывание (есть хотя бы одно значение 1 в
Задание 4 Чтобы составить наглядное представление о графе, достаточно вообразить некоторое множество точек плоскости или пространства и множество отрезков, соединяющих все или некоторые из этих точек. Точки множества называют вершинами, а отрезки, их соединяющие,— дугами, если указано, какая вершина является начальной, и ребрами, если ориентация не указана. Два ребра, связывающие одну и ту же пару вершин, называются кратными. Ребро, связывающее вершину саму с собой, называется петлей. Граф, состоящий из дуг, называют ориентированным (орграфом), а образованный ребрами — неориентированным. Степенью вершины Формально граф При большом числе элементов рисунок графа теряет наглядность. В таком случае граф целесообразно задать матричным способом. Матрица смежности вершин орграфа — это квадратная матрица В случае неориентированного графа ему вместе с ребром Матрица смежности дуг орграфа — это квадратная матрица Матрицей смежности ребер неориентированного графа является матрица Матрица инцидентности орграфа — это прямоугольная матрица размерности
Пример.
|

 называют число дуг (ребер), которым она принадлежит (инцидентна), при этом петли считаются дважды. Степень вершины обозначают
называют число дуг (ребер), которым она принадлежит (инцидентна), при этом петли считаются дважды. Степень вершины обозначают  . Для орграфов различают полустепень захода
. Для орграфов различают полустепень захода  вершины
вершины 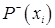 (количество дуг, исходящих из
(количество дуг, исходящих из  определяется заданием двух множеств
определяется заданием двух множеств  и
и  , где
, где 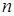 -го порядка (
-го порядка (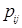 матрицы равны числу дуг, направленных из
матрицы равны числу дуг, направленных из  -й вершины в
-й вершины в  -ю. Если орграф состоит из однократных дуг, то элементы матрицы равны либо 0, либо 1. Если орграф состоит из однократных дуг, то элементы матрицы равны либо 0, либо 1.
-ю. Если орграф состоит из однократных дуг, то элементы матрицы равны либо 0, либо 1. Если орграф состоит из однократных дуг, то элементы матрицы равны либо 0, либо 1.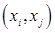 принадлежит и ребро
принадлежит и ребро  , поэтому матрица будет симметрической. Справедливо и обратное заключение: любой симметрической матрице с целыми неотрицательными элементами можно поставить в соответствие граф.
, поэтому матрица будет симметрической. Справедливо и обратное заключение: любой симметрической матрице с целыми неотрицательными элементами можно поставить в соответствие граф.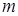 -го порядка (
-го порядка ( равны 1, если дуга
равны 1, если дуга  непосредственно предшествует дуге
непосредственно предшествует дуге  , и 0 в остальных случаях.
, и 0 в остальных случаях. , строки которой соответствуют вершинам, а столбцы — дугам орграфа. Элементы
, строки которой соответствуют вершинам, а столбцы — дугам орграфа. Элементы  равны 1, если дуга
равны 1, если дуга  , если дуга заходит в
, если дуга заходит в 


