Файл-функции и файл-программы
Файл-функции и файл-программы Встроенный язык программирования MatLab достаточно прост, он содержит необходимый минимум конструкций, которые описаны в следующем параграфе. Прежде чем программировать в MatLab, необходимо понять, что все программы могут быть либо файл-функциями, либо файл-программами. Файл-программа является текстовым файлом с расширением m (M-файлом), в котором записаны команды и операторы MatLab. Разберем, как создать простую файл-программу. В MatLab имеется редактор M-файлов, для запуска которого следует нажать кнопку New M-file на панели инструментов рабочей среды, либо выбрать в меню File в пункте New подпункт M-file. На экране появляется окно редактора. Наберите в нем какие-либо команды, например для построения графика (см. листинг 5.1): Листинг 5.1. Простейшая файл-программа x=[-1:0.01:1]; y=exp(x); plot(x,y) grid on title('Экспоненциальная функция') Для запуска программы или ее части есть несколько способов. Первый, самый простой — выделить операторы при помощи мыши, удерживая левую кнопку, или при помощи клавишы[1] <Shift> со стрелками, <PageUp>, <PageDown> и выбрать в меню View пункт Evaluate Selection (или нажать <F9>). Выделенные операторы выполняются последовательно, точно так же, как если бы они были набраны в командной строке. Очевидно, что работать в M-файле удобнее, чем из командной строки, поскольку можно сохранить программу, добавить операторы, выполнять отдельные команды не пробегаясь по истории команд, как в случае командной строки. После того, как программа сохранена в M-файле, к примеру в myprog.m, для ее запуска можно использовать пункт Tools меню Run, либо просто набрать в командной строке имя M-файла (без расширения) и нажать <Enter>, то есть выполнить, как обычную команду MatLab. При таких способах запуска программы следует учесть важное обстоятельство — путь к каталогу с M-файлом должен быть известен MatLab. Сделайте каталог с файлом myprog текущим. § В MatLab 5.3 в меню File рабочей среды перейдите к пункту Set Path… Появляется диалоговое окно Path Browser (навигатор путей). В строке ввода Current Directory установите требуемый каталог. Воспользуйтесь кнопкой, расположенной справа от строки ввода, для выбора каталога. § В MatLab 6.x установка текущего каталога производится из окна Current Directory рабочей среды. Если это окно отсутствует, то следует выбрать пункт Current Directory меню View рабочей среды. Для выбора желаемого каталога на диске нажмите кнопку, расположенную справа от раскрывающегося списка. Когда текущий каталог установлен, то все M-файлы, находящиеся в нем, могут быть запущены из командной строки, либо из редактора M-файлов. Все переменные файл-программы после ее запуска доступны в рабочей среде, т. е. являются глобальными. Убедитесь в этом, выполнив команду whos. Более того, файл-программа может использовать переменные рабочей среды. Например, если была введена команда: » a=[0.1 0.4 0.3 1.9 3.3]; то файл-программа, содержащая строку bar(а), построит столбцевую диаграмму вектора a (разумеется, если он не был переопределен в самой файл-программе). Файл-функции отличаются от файл-программ тем, что они могут иметь входные и выходные аргументы, а все переменные, определенные внутри файл-функции, являются локальными и не видны в рабочей среде. M-файл, содержащий файл-функцию, должен начинаться с заголовка, после него записываются операторы MatLab. Заголовок состоит из слова function, списка выходных аргументов, имени файл-функции и списка входных аргументов. Аргументы в списках разделяются запятой. Листинг 5.2 содержит пример простейшей файл-функции с двумя входными и одним выходным аргументами. Листинг 5.2. Файл-функция mysum function c=mysum(a,b) c=a+b; Наберите этот пример в новом файле в редакторе и сохраните его. Обратите внимание, что MatLab предлагает в качестве имени M-файла название файл-функции, т.е. mysum.m. Всегда сохраняйте файл-функцию в M-файле, имя которого совпадает с именем файл-функции! Убедитесь, что каталог с файлом mysum.m является текущим и вызовите файл-функцию mysum из командной строки: » s=mysum(2,3) s = При вызове файл-функции mysum произошли следующие события: § входной аргумент a получил значение 2; § входной аргумент b стал равен 3; § сумма a и b записалась в выходной аргумент c; § значение выходного аргумента c получила переменная s рабочей среды и результат вывелся в командное окно. Заметьте, что оператор c=a+b в файл-функции mysum завершен точкой с запятой для подавления вывода локальной переменной c в командное окно. Для просмотра значений локальных переменных при отладке файл-функций, очевидно, не следует подавлять вывод на экран значений требуемых переменных. Практически все функции MatLab являются файл-функциями и хранятся в одноименных M-файлах. Функция sin допускает два варианта вызова: sin(x) и y=sin(x), в первом случае результат записывается в ans, а во втором — в переменную y. Наша функция mysum ведет себя точно так же. Более того, входными аргументами mysum могут быть массивы одинаковых размеров или массив и число. Разберем теперь, как создать файл-функцию с несколькими выходными аргументами. Список выходных аргументов в заголовке файл-функции заключается в квадратные скобки, сами аргументы отделяются запятой. В качестве примера на листинге 5.3 приведена файл-функция quadec, которая по заданным коэффициентам квадратного уравнения находит его корни. Листинг 5.3. Файл-функция для решения квадратного уравнения function [x1,x2]=quadeq(a,b,c) D=b^2-4*a*c; x1=(b+sqrt(D))/(2*a); x2=(b-sqrt(D))/(2*a); При вызове quadeq из командной строки используйте квадратные скобки для указания переменных, в которые будут занесены значения корней: » [r1,r2]=quadeq(1,3,2) r1 = r2 = Заметьте, что файл-функцию quadec можно вызвать без выходных аргументов, или только с одним выходным аргументом. В этом случае вернется только первый корень. Файл-функция может и не иметь входных или выходных аргументов, заголовки таких файл-функций приведены ниже: function noout(a,b), function [v,u]=noin, function noarg() Умение писать собственные файл-функции и файл-программы необходимо как при программировании в MatLab, так и при решении различных задач средствами MatLab (в частности, поиска корней уравнений, интегрирования, оптимизации[2]). Разберем только один пример, связанный с построением графика функции Листинг 5.4. Файл-функция myfun function y=myfun(x); y=exp(-x).*(sin(x)+0.1*sin(100*pi*x)); График » x=[0:0.01:1]; » y=myfun(x); » plot(x,y) В результате получается график, приведенный на рис. 5.1, а, который, очевидно, неверен. Действительно, при вычислении значений функции на отрезке » figure » fplot('myfun',[0,1]) Получился график, точно отражающий поведение функции (рис. 5.1, б). а) б)
Рис. 5.1. Задания для самостоятельной работы Написать файл-функции и построить графики на заданном отрезке при помощи plot (с шагом 0.05) и fplot для следующих функций: Варианты 1. 3. 5.
7. 9. 10. Задания для самостоятельной работы Написать файл-функцию для решения поставленной задачи. Варианты 1. Написать файл-функцию, которая по заданному вектору определяет номер его элемента с наибольшим отклонением от среднего арифметического всех элементов вектора. 2. Написать файл-функцию, возвращающую сумму всех элементов вектора с нечетными индексами. 3. Написать файл-функцию, вычисляющую максимальное значение среди диагональных элементов заданной матрицы. 4. Написать файл-функцию, переставляющую первый столбец квадратной матрицы с ее диагональю. 5. Написать файл-функцию, которая суммирует все внедиагональные элементы заданной матрицы. 6. Написать файл-функцию, заменяющую максимальный элемент вектора средним значением всех его элементов. 7. Написать файл-функцию, заменяющую элемент матрицы с индексами 1,1 произведением всех элементов матрицы. 8. Написать файл-функцию, которая строит многоугольник (замкнутый) по заданным векторам x и y с координатами вершин. 9. Написать файл-функцию, которая отображает элементы заданного вектора синими маркерами, а максимальный элемент — красным и возвращает значение и номер максимального элемента. 10. Написать файл-функцию, переводящую время в секундах в часы, минуты и секунды.
[2] Использование численных методов MatLab выходит за рамки этого пособия.
|

 на отрезке
на отрезке  . Запрограммируйте файл-функцию myfun для вычисления
. Запрограммируйте файл-функцию myfun для вычисления  . Используйте поэлементные операции (см. листинг 5.4) для того, чтобы myfun можно было вызывать от вектора значений аргумента и получать вектор соответствующих значений функции.
. Используйте поэлементные операции (см. листинг 5.4) для того, чтобы myfun можно было вызывать от вектора значений аргумента и получать вектор соответствующих значений функции. все время обращалось в ноль и plot построила график не
все время обращалось в ноль и plot построила график не 

 . 2.
. 2. 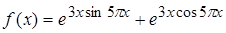
 .
.
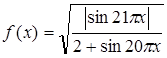


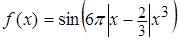



 .
.


