Задача № 2. Вычислить интеграл по формуле трапеций при , оценить погрешность результата 2 способами: а) по правилу Рунге; б) с помощью двойного просчетаВычислить интеграл по формуле трапеций при
Решение: Расчетная формула при числе разбиений
вычисления в среде MathCad
Найти наименьший положительный корень уравнения комбинированным методом с точностью до 0,0001
Решение: Формулы комбинированного метода: Пусть дано уравнение f(x) = 0, корень отделен на отрезке [a, b]. Рассмотрим случай, когда f ‘(x) f ’’(x)>0.
В этом случае метод хорд дает приближенное значение корня с недостатком (конец b неподвижен), а метод касательных – с избытком (за начальное приближение берем точку b). Тогда вычисления следует проводить по формулам:
Теперь корень ξ; заключен в интервале [a1, b1]. Применяя к этому отрезку комбинированный метод, получим:
Если же f ‘(x) f ’’(x)<0, то, рассуждая аналогично, получим следующие формулы для уточнения корня уравнения:
Вычислительный процесс прекращается, как только выполнится условие: Решение в MathCAD:
Итак, решение уравнения
|
, оценить погрешность результата 2 способами: а) по правилу Рунге; б) с помощью двойного просчета.
.
:
.
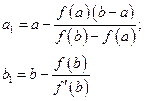
