Основные уравнения динамики
Аналитические модели являются познавательными моделями. Существенной особенностью этих моделей является отражение механизма явления в структуре оператора модели, то есть всех причинно-следственных связей, имеющихся у объекта. Построение любой математической модели начинают с физического описания объекта моделирования. При этом выделяют "элементарные" процессы, протекающие в объекте моделирования, которые подлежат отражению в модели, и формулируют основные допущения, принимаемые при их описании. "Элементарные" здесь не означает "простейший", а лишь то, что эти процессы являются составляющими более сложных процессов. Обычно под "элементарным" понимается процесс, относящийся к определенному классу явлений, например, массообмен, теплопередача и т.д. Обычно принимаются во внимание следующие "элементарные" процессы: движение потоков фаз, массообмен между фазами, теплопередача, изменение агрегатного состояния, химические превращения. Перечень учитываемых элементарных процессов определяет совокупность явлений, описывающих объект, которые включают в математическую модель. Основная технология теплоэнергетической промышленности базируется на физических процессах, элементарными составляющими которых являются: - механические процессы – механическая обработка твердых материалов; - гидродинамические процессы (транспорт жидкости и газа); - тепловые процессы (нагрев и охлаждение); - массообменные процессы (испарение и конденсация). Закономерности протекания всех этих процессов тесно связаны с условиями движения среды, в которой они происходят, и которые определяются законами гидро-, газодинамики. Кроме того, они базируются (кроме первого) на элементарных процессах переноса вещества и энергии между отдельными частями системы. Закономерности такого переноса изучает термодинамика. (Изучение механических процессов базируется на законах теории упругости и механики твердого тела). То есть общей теоретической основой для моделирования большей части технологических процессов является гидро- и термодинамика. Общность научных основ элементарных стадий технологических процессов определяет и общность принципов их анализа и последующего построения допустимого класса их моделей. Задача построения математической модели объекта в общем случае сводится к определению оператора системы, определяющего изменение выходной величины при произвольном изменении входного воздействия. Аналитические методы определения характеристик объектов регулирования основаны на составлении их дифференциальных уравнений. Составление дифференциального уравнения базируется на использовании основных физических законов: сохранения массы, энергии и количества движения. Состояние систем обычно выражают посредством законов термодинамики. Первый закон термодинамики имеет единую математическую и физическую формулировку: Изменение во времени субстанции в элементарном объеме равно сумме притока и стока субстанции через его поверхность. Математически это можно описать дифференциальным уравнением в переменных Эйлера:
состоящем из локального изменения переносимой величины Этот закон формулирует неуничтожимость материи и ее движения и записывается через совокупность законов сохранения массы, энергии, количества движения. Для описания свойств процессов в объектах с распределенными параметрами законы сохранения должны быть выражены в строгом виде. Закон сохранения массы. Это основной закон классической механики: масса любой части материальной системы, находящейся в движении, не зависит от времени и является постоянной величиной. То есть полная производная от массы любой части рассматриваемой системы равна 0:
ρ(х) – плотность вещества, Х = (х1,х2,х3) – координаты точки евклидова пространства, Ω; – произвольный объем системы, dv=dх1dх2dх3 – дифференциал объема. (2.1.2) – интегральная форма закона сохранения массы. Дифференциальная форма закона сохранения:
где w – скорость центра масс. В механике сплошных сред (2.1.3) называют уравнением неразрывности (сплошности). В такой же форме записывается уравнение сохранения массы и для многих компонент, если между ними не происходит химических реакций, и отсутствуют фазовые переходы. В противном случае в правую часть (2.3) включают удельные мощности источника (mk), характеризующего скорость возникновения какого-либо компонента за счет уничтожения других:
где k – номер компонента, wk, ρ;k – относительная скорость и плотность компонента. Закон сохранения количества движения: скорость изменения количества движения любой части материальной системы, находящейся в движении, равна сумме всех внешних сил. Количество движения элемента системы массы m, движущегося со скоростью w есть вектор
Разделим внешние силы на две группы: 1 – сумма сил Fv, обусловленных внешними силовыми полями (гравитационные, электрические, магнитные) и действующие на единицу массы объема Ω;; 2 – силы Fs, действующие на единицу поверхности объема Ω;. Тогда:
Имеем
или в дифференциальной форме
Закон сохранения энергии: при бесконечно малом подводе тепла δQ к изолированной системе и совершении этой системой бесконечно малой работы δA, энергия системы изменяется на величину de = δQ – δA:
Обычно это уравнение используется в виде: где μ; – коэффициент динамической вязкости, Ф – диссипативная функция Релея, учитывающая рассеяние кинетической энергии вследствие действия сил вязкости. Эти уравнения должны быть дополнены еще одним, выражающим второй закон термодинамики, который характеризует возрастание энтропии в системе, в которой происходит движение вещества или энергии. Мы их рассмотрим в виде следующих законов переноса массы и энергии. Система уравнений должна быть дополнена уравнением состояния
Вместе с краевыми условиями эти уравнения полностью описывают поведение динамической системы в любой момент времени. Общим для всех математических моделей является то, что число уравнений, включаемых в математическое описание, должно быть равно числу переменных, находимых в результате моделирования. Важной особенностью математического описания, содержащего обыкновенные дифференциальные уравнения, является необходимость задания начальных условий. Для уравнений в частных производных наряду с начальными нужно также задавать граничные условия, в общем случае являющиеся функциями времени (так как параметры распределены по нескольким координатам). В ряде случаев вместо описания объекта дифференциальными уравнениями используют его описание системой конечно-разностных уравнений. При подобных преобразованиях возникает погрешность, которую необходимо учитывать при оценке результатов моделирования.
|

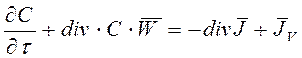 (2.1.1)
(2.1.1) , ее конвективного переноса
, ее конвективного переноса  , диффузионного переноса
, диффузионного переноса  и источников (стоков) величины
и источников (стоков) величины 
 (2.1.2)
(2.1.2) (2.1.3)
(2.1.3) (2.1.4)
(2.1.4)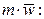
 (2.1.5)
(2.1.5) (2.1.6)
(2.1.6)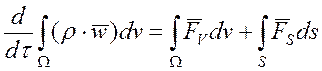 (2.1.7)
(2.1.7)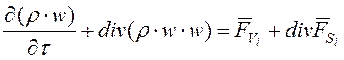 (2.1.8)
(2.1.8) (2.1.9)
(2.1.9) (2.1.10)
(2.1.10) (2.1.23)
(2.1.23)


