Задание № 2
Даны функции g(x) и h(x,y,z). Определить, какая функция f(x,y) получается из них с помощью операции примитивной рекурсии. 2.1. g(x)=x, h(x,y,z)=z+x 2.2. g(x)=x, h(x,y,z)=z 2.3. g(x)=x, h(x,y,z)=x 2.5. g(x)=2, h(x,y,z)=z+x 2.6. g(x)=2, h(x,y,z)=z 2.7. g(x)=2, h(x,y,z)=x 2.9. g(x)=x, h(x,y,z)=z+2x 2.10. g(x)=2, h(x,y,z)=2zx
Задание № 3
В канторовской нумерации определить номер тройки <х 1.1. <1,2,4>; n=21; 1.2. <2,1,3>; n=15; 1.3. <1,1,8>; n=25; 1.4. <3,2,1>; n=30; 1.5. <2,3,5>; n=28; 1.6. <3,1,2>; n=20; 1.7. <4,2,1>; n=35; 1.8. <2,0,9>; n=38; 1.9. <3,5,0>; n=40; 1.10. <4,0,9>; n=45;
Задание № 4
Дан алфавит А= 1.1. 1.3. 1.5. 1.7. 1.9.
Задание № 5.
В алфавите А= 5.1 – 5.5 F( 5.6. – 5.10 F(
|
2.4. g(x)=x, h(x,y,z)=zx
,х 
,х 
> и тройку с номером n.
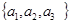. Определить словарный номер С (
) слова 
(n), имеющее номер n.
показать примитивную рекурсивность словарной функции.
)= 
