У курицы чей клюв? – Куриный. У петуха – петушиный.
У гуся – гусиный. У утки – утиный.
У индюка – индюшиный (индюшачий)
Птицы, которые в воде плавают – водоплавающие (утки, гуси).
Закончи предложение:
У курицы гребешок маленький, а у петуха - … (большой).
У петуха на лапках когти и шпоры, а у гуся на лапках когти и …(перепонки).
У курицы шея короткая, а у гуся - … (длинная).
У петуха хвост длинный, а у курицы - … (короткий).
Ответь на вопросы:
1. Для чего гусю и утке нужны перепонки?
2. Почему человек разводит птиц?
3. Кто лишний и почему: гусь, селезень, кот, петух?
4. ………………………. Цыплёнок, утёнок, гусёнок, курица?
Кого ты видишь? Кто лишний? Объясни свой выбор. Раскрась только домашних птиц.
Домашняя работа № 12
1. Найдите корень уравнения:  В ответе запишите наибольший отрицательный корень.
2. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.
2. Найдите корень уравнения:  В ответе запишите наибольший отрицательный корень.
3. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.
3. Найдите корень уравнения: 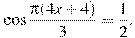 В ответе запишите наибольший отрицательный
4. Решите уравнение В ответе запишите наибольший отрицательный
4. Решите уравнение  . В ответе напишите наибольший отрицательный корень. . В ответе напишите наибольший отрицательный корень.
| 5. Решите уравнение  . В ответе напишите наименьший положительный корень.
6. Решите уравнение . В ответе напишите наименьший положительный корень.
6. Решите уравнение  . В ответе напишите наименьший положительный корень.
7. Решите уравнение . В ответе напишите наименьший положительный корень.
7. Решите уравнение  . В ответе напишите наименьший положительный корень.
8. Решите уравнение . В ответе напишите наименьший положительный корень.
8. Решите уравнение 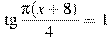 . В ответе напишите наименьший положительный корень. . В ответе напишите наименьший положительный корень.
|
Домашняя работа № 13
1. Решите уравнение  . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
2. Найдите корень уравнения: . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
2. Найдите корень уравнения: 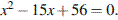 Если уравнение имеет более одного корня, укажите меньший из них.
3.Найдите корень уравнения: Если уравнение имеет более одного корня, укажите меньший из них.
3.Найдите корень уравнения:  . .
| 4. Найдите корень уравнения:  .
5. Решите уравнение .
5. Решите уравнение  .
6. Найдите корень уравнения: .
6. Найдите корень уравнения:  .
7.Найдите корень уравнения: .
7.Найдите корень уравнения: 
| 8. Решите уравнение  . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
9. Найдите корень уравнения: . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
9. Найдите корень уравнения:  10.Решите уравнение
10.Решите уравнение  . Если уравнение имеет более одного корня, в ответе запишите больший из корней. . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
|
Зачетная работа № 4
1. Решите уравнение  . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
2. Найдите корень уравнения 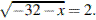
3. Найдите корень уравнения  .
.
4. Найдите корень уравнения:  .
.
5. Решите уравнение  . В ответе напишите наименьший положительный корень.
. В ответе напишите наименьший положительный корень.
6. Найдите корень уравнения 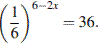
7. Найдите корень уравнения  .
.
8. Найдите корень уравнения 
9. Найдите корень уравнения: 
10. Решите уравнение 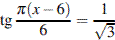 . В ответе напишите наименьший положительный корень.
. В ответе напишите наименьший положительный корень.
Домашняя работа № 14
1.№ 27500. На рисунке изображен график производной функции f(x), определенной на интервале (−2; 12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.

| 2 27494. На рисунке изображен график производной функции f(x), определенной на интервале (−7; 14). Найдите количество точек максимума функции f(x) на отрезке [−6; 9].

|
3 27496. На рисунке изображен график производной функции f(x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции f(x) на отрезке [−10; 10].

| 4 27502. На рисунке изображен график производной функции f(x), определенной на интервале (−4; 8). Найдите точку экстремума функции f(x) на отрезке [−2; 6].

|
5.№ 27499. На рисунке изображен график производной функции f(x), определенной на интервале (−11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

| 6.На рисунке изображен график производной функции  , определенной на интервале , определенной на интервале  . В какой точке отрезка . В какой точке отрезка   принимает наименьшее значение? принимает наименьшее значение?

|
Домашняя работа № 15
1 119971. На рисунке изображен график функции f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых производная функции f(x) равна 0.
285 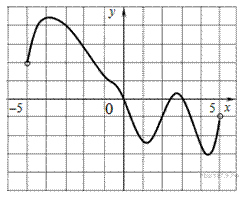
| 2.№ 27497. На рисунке изображен график производной функции f(x), определенной на интервале (−7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
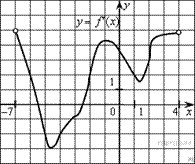
|
3.№ 27488. На рисунке изображен график функции  , определенной на интервале (−5; 5). Определите количество целых точек, в которых производная функции , определенной на интервале (−5; 5). Определите количество целых точек, в которых производная функции  отрицательна. отрицательна.

| 4.№ 27501. На рисунке изображен график производной функции f(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = −2 x −11 или совпадает с ней.

|
5.№ 27489. На рисунке изображен график функции y=f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.

| 6.№ 27505. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x 0. Найдите значение производной функции f(x) в точке x 0.

|
Домашняя работа № 16
1. Найдите наименьшее значение функции  на отрезке
на отрезке  .
.
2. Найдите наименьшее значение функции  на отрезке
на отрезке  .
.
3. Найдите точку минимума функции  .
.
4. Найдите точку минимума функции  .
.
5. Найдите наибольшее значение функции 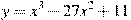 на отрезке
на отрезке  .
.
6. Найдите наибольшее значение функции  на отрезке
на отрезке  .
.
7. Найдите точку максимума функции  .
.
8.  Найдите точку максимума функции
Найдите точку максимума функции 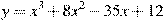 .
.
Зачетная работа № 5
1. На рисунке изображен график функции  , определенной на интервале
, определенной на интервале  . Определите количество целых точек, в которых производная функции
. Определите количество целых точек, в которых производная функции  положительна.
положительна.

2.На рисунке изображен график  — производной функции
— производной функции  , определенной на интервале
, определенной на интервале  . В какой точке отрезка
. В какой точке отрезка 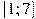 функция
функция  принимает наименьшее значение.
принимает наименьшее значение.

 3.На рисунке изображен график функции
3.На рисунке изображен график функции  , определенной на интервале
, определенной на интервале  . Определите количество целых точек, в которых производная функции
. Определите количество целых точек, в которых производная функции  отрицательна.
отрицательна.
4.На рисунке изображен график функции  , определенной на интервале
, определенной на интервале  . Найдите количество точек, в которых касательная к графику функции параллельна прямой
. Найдите количество точек, в которых касательная к графику функции параллельна прямой  .
.

5.На рисунке изображен график функции  , определенной на интервале
, определенной на интервале  . Найдите количество точек, в которых касательная к графику функции параллельна прямой
. Найдите количество точек, в которых касательная к графику функции параллельна прямой  .
.

6.На рисунке изображен график функции  , определенной на интервале
, определенной на интервале  . Найдите сумму точек экстремума функции
. Найдите сумму точек экстремума функции  .
.

7.На рисунке изображен график  — производной функции
— производной функции  , определенной на интервале
, определенной на интервале  . В какой точке отрезка
. В какой точке отрезка  функция
функция  принимает наибольшее значение?
принимает наибольшее значение?

8.На рисунке изображен график  — производной функции
— производной функции  , определенной на интервале
, определенной на интервале 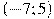 . В какой точке отрезка
. В какой точке отрезка  функция
функция  принимает наименьшее значение?
принимает наименьшее значение?

9.На рисунке изображен график  — производной функции
— производной функции  , определенной на интервале
, определенной на интервале  . Найдите количество точек минимума функции
. Найдите количество точек минимума функции  , принадлежащих отрезку
, принадлежащих отрезку  .
.

10.На рисунке изображен график  — производной функции
— производной функции  , определенной на интервале
, определенной на интервале  . Найдите количество точек экстремума функции
. Найдите количество точек экстремума функции  , принадлежащих отрезку
, принадлежащих отрезку  .
.
 11. На рисунке изображен график
11. На рисунке изображен график  — производной функции
— производной функции  , определенной на интервале
, определенной на интервале  . Найдите промежутки возрастания функции
. Найдите промежутки возрастания функции  . В ответе укажите сумму целых точек, входящих в эти промежутки.
. В ответе укажите сумму целых точек, входящих в эти промежутки.

12. На рисунке изображен график  — производной функции
— производной функции  , определенной на интервале
, определенной на интервале  . Найдите промежутки убывания функции
. Найдите промежутки убывания функции  . В ответе укажите сумму целых точек, входящих в эти промежутки.
. В ответе укажите сумму целых точек, входящих в эти промежутки.

13. На рисунке изображен график  — производной функции
— производной функции  , определенной на интервале
, определенной на интервале  . Найдите промежутки возрастания функции
. Найдите промежутки возрастания функции  . В ответе укажите сумму целых точек, входящих в эти промежутки.
. В ответе укажите сумму целых точек, входящих в эти промежутки.

 14. На рисунке изображен график
14. На рисунке изображен график  — производной функции
— производной функции  , определенной на интервале
, определенной на интервале  . Найдите промежутки возрастания функции
. Найдите промежутки возрастания функции  . В ответе укажите длину наибольшего из них.
. В ответе укажите длину наибольшего из них.
 15. На рисунке изображен график
15. На рисунке изображен график  — производной функции
— производной функции  , определенной на интервале
, определенной на интервале 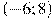 . Найдите количество точек, в которых касательная к графику функции
. Найдите количество точек, в которых касательная к графику функции  параллельна прямой
параллельна прямой  или совпадает с ней.
или совпадает с ней.
16. На рисунке изображен график  — производной функции
— производной функции  , определенной на интервале
, определенной на интервале  . Найдите точку экстремума функции
. Найдите точку экстремума функции  , принадлежащую отрезку
, принадлежащую отрезку  .
.
 17. На рисунке изображен график
17. На рисунке изображен график  — производной функции
— производной функции  , определенной на интервале
, определенной на интервале 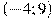 . Найдите точку экстремума функции
. Найдите точку экстремума функции  , принадлежащую отрезку
, принадлежащую отрезку  .
.

 18. На рисунке изображены график функции
18. На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции  в точке
в точке  .
.
19. На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции  в точке
в точке  .
.
Зачетная работа № 6
1. Найдите наибольшее значение функции  на отрезке
на отрезке  .
.
2. Найдите наименьшее значение функции 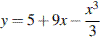 на отрезке
на отрезке  .
.
3. Найдите наименьшее значение функции  на отрезке
на отрезке  .
.
4. Найдите наибольшее значение функции 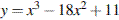 на отрезке
на отрезке  .
.
5. Найдите точку максимума функции  .
.
6. Найдите точку минимума функции. 
Домашняя работа № 17
1. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых.
2. В чемпионате по гимнастике участвуют 40 спортсменок: 12 из Аргентины, 9 из Бразилии, остальные — из Парагвая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Парагвая.
3. В среднем из 500 садовых насосов, поступивших в продажу, 4 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
4. Фабрика выпускает сумки. В среднем на 80 качественных сумок приходится одна сумка со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
5. В соревнованиях по толканию ядра участвуют 4 спортсмена из Эстонии, 6 спортсменов из Латвии, 3 спортсмена из Литвы и 7 — из Польши. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Литвы.
6. Научная конференция проводится в 4 дня. Всего запланировано 40 докладов — первые два дня по 11 докладов, остальные распределены поровну между третьим и четвертым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
7. Конкурс исполнителей проводится в 3 дня. Всего заявлено 50 выступлений — по одному от каждой страны. В первый день 34 выступления, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
8. В фирме такси в данный момент свободно 20 машин: 10 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси.
9. На тарелке 16 пирожков: 7 с рыбой, 5 с вареньем и 4 с вишней. Юля наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
10. Из множества натуральных чисел от 25 до 39 наудачу выбирают одно число. Какова вероятность того, что оно делится на 5?
Домашняя работа № 18
1.
В пачке 500 листов бумаги формата А4. За неделю в офисе расходуется 1200 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 4 недели?
2. Цена на электрический чайник была повышена на 24 % и составила 2480 рублей. Сколько рублей стоил чайник до повышения цены?
3. На рисунке показано изменение температуры воздуха на протяженаятрех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 22 января. Ответ дайте в градусах Цельсия.

4.  В первом банке один австралийский доллар можно купить за 28,6 рубля. Во втором банке 120 долларов — за 3420 рублей. В третьем банке 40 долларов стоят 1148 рублей. Какую наименьшую сумму (в рублях) придется заплатить за 30 австралийских долларов?
В первом банке один австралийский доллар можно купить за 28,6 рубля. Во втором банке 120 долларов — за 3420 рублей. В третьем банке 40 долларов стоят 1148 рублей. Какую наименьшую сумму (в рублях) придется заплатить за 30 австралийских долларов?
5. Две стороны изображенного на рисунке прямоугольника  равны 6 и 8. Диагонали пересекаются в точке
равны 6 и 8. Диагонали пересекаются в точке  . Найдите длину суммы векторов
. Найдите длину суммы векторов  и
и  .
.
6. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
7. Решите уравнение  . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
8.  Большее основание равнобедренной трапеции равно 34. Боковаяясторона равна 14. Синус острого угла равен
Большее основание равнобедренной трапеции равно 34. Боковаяясторона равна 14. Синус острого угла равен  . Найдите меньшее основание.
. Найдите меньшее основание.
9. На рисунке изображен график производной функции f(x), определенной на интервале (−16; 4). Найдите количество точек экстремума функции f(x) на отрезке [−14; 2].

10.  Найдите площадь поверхности многогранника изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника изображенного на рисунке (все двугранные углы прямые).
11. Найдите значение выражения  .
.
12. Для сматывания кабеля на заводе используют лебeдку, которая равноускоренно наматывает кабель на катушку. Угол, на который поворачивается катушка изменяется со временем по закону  , где
, где 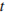 — время в минутах,
— время в минутах,  мин — начальная угловая скорость вращения катушки, а
мин — начальная угловая скорость вращения катушки, а  мин
мин  — угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки
— угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки  достигнет 4050°. Определите время после начала работы лебeдки, не позже которого рабочий должен проверить еe работу. Ответ выразите в минутах.
достигнет 4050°. Определите время после начала работы лебeдки, не позже которого рабочий должен проверить еe работу. Ответ выразите в минутах.

13. Объем прямоугольного параллелепипеда равен 240. Площадь одной его грани равна 24. Найдите ребро параллелепипеда, перпендикулярное этой грани.
14. Катер в 10:00 вышел из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 2 часа 30 минут, катер отправился назад и вернулся в пункт А в 18:00. Определите (в км/час) скорость течения реки, если известно, что собственная скорость катера равна 11 км/ч.
15. Найдите наибольшее значение функции  на отрезке
на отрезке  .
.


 В ответе запишите наибольший отрицательный корень.
2. Найдите корень уравнения:
В ответе запишите наибольший отрицательный корень.
2. Найдите корень уравнения:  В ответе запишите наибольший отрицательный корень.
3. Найдите корень уравнения:
В ответе запишите наибольший отрицательный корень.
3. Найдите корень уравнения: 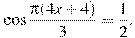 В ответе запишите наибольший отрицательный
4. Решите уравнение
В ответе запишите наибольший отрицательный
4. Решите уравнение  . В ответе напишите наибольший отрицательный корень.
. В ответе напишите наибольший отрицательный корень.
 . В ответе напишите наименьший положительный корень.
6. Решите уравнение
. В ответе напишите наименьший положительный корень.
6. Решите уравнение  . В ответе напишите наименьший положительный корень.
7. Решите уравнение
. В ответе напишите наименьший положительный корень.
7. Решите уравнение  . В ответе напишите наименьший положительный корень.
8. Решите уравнение
. В ответе напишите наименьший положительный корень.
8. Решите уравнение 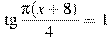 . В ответе напишите наименьший положительный корень.
. В ответе напишите наименьший положительный корень.
 . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
2. Найдите корень уравнения:
. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
2. Найдите корень уравнения: 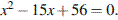 Если уравнение имеет более одного корня, укажите меньший из них.
3.Найдите корень уравнения:
Если уравнение имеет более одного корня, укажите меньший из них.
3.Найдите корень уравнения:  .
.
 .
5. Решите уравнение
.
5. Решите уравнение  .
6. Найдите корень уравнения:
.
6. Найдите корень уравнения:  .
7.Найдите корень уравнения:
.
7.Найдите корень уравнения: 
 . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
9. Найдите корень уравнения:
. Если уравнение имеет более одного корня, в ответе запишите больший из корней.
9. Найдите корень уравнения:  10.Решите уравнение
10.Решите уравнение  . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
. Если уравнение имеет более одного корня, в ответе запишите больший из корней.
 . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.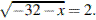
 .
. . В ответе напишите наименьший положительный корень.
. В ответе напишите наименьший положительный корень.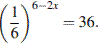
 .
.

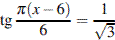 . В ответе напишите наименьший положительный корень.
. В ответе напишите наименьший положительный корень.




 , определенной на интервале
, определенной на интервале  . В какой точке отрезка
. В какой точке отрезка 



 , определенной на интервале (−5; 5). Определите количество целых точек, в которых производная функции
, определенной на интервале (−5; 5). Определите количество целых точек, в которых производная функции 



 на отрезке
на отрезке  .
. на отрезке
на отрезке  .
. .
. .
.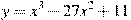 на отрезке
на отрезке  .
. на отрезке
на отрезке  .
. .
. Найдите точку максимума функции
Найдите точку максимума функции 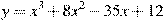 .
. , определенной на интервале
, определенной на интервале  . Определите количество целых точек, в которых производная функции
. Определите количество целых точек, в которых производная функции  положительна.
положительна.
 — производной функции
— производной функции 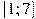 функция
функция 
 3.На рисунке изображен график функции
3.На рисунке изображен график функции  . Определите количество целых точек, в которых производная функции
. Определите количество целых точек, в которых производная функции  . Найдите количество точек, в которых касательная к графику функции параллельна прямой
. Найдите количество точек, в которых касательная к графику функции параллельна прямой  .
.
 . Найдите количество точек, в которых касательная к графику функции параллельна прямой
. Найдите количество точек, в которых касательная к графику функции параллельна прямой  .
.
 . Найдите сумму точек экстремума функции
. Найдите сумму точек экстремума функции 
 . В какой точке отрезка
. В какой точке отрезка  функция
функция 
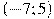 . В какой точке отрезка
. В какой точке отрезка  функция
функция 
 . Найдите количество точек минимума функции
. Найдите количество точек минимума функции  .
.
 . Найдите количество точек экстремума функции
. Найдите количество точек экстремума функции  .
. 11. На рисунке изображен график
11. На рисунке изображен график  . Найдите промежутки возрастания функции
. Найдите промежутки возрастания функции 
 . Найдите промежутки убывания функции
. Найдите промежутки убывания функции 
 . Найдите промежутки возрастания функции
. Найдите промежутки возрастания функции 
 14. На рисунке изображен график
14. На рисунке изображен график  . Найдите промежутки возрастания функции
. Найдите промежутки возрастания функции  15. На рисунке изображен график
15. На рисунке изображен график 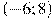 . Найдите количество точек, в которых касательная к графику функции
. Найдите количество точек, в которых касательная к графику функции  или совпадает с ней.
или совпадает с ней. . Найдите точку экстремума функции
. Найдите точку экстремума функции  .
. 17. На рисунке изображен график
17. На рисунке изображен график 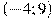 . Найдите точку экстремума функции
. Найдите точку экстремума функции  .
.
 18. На рисунке изображены график функции
18. На рисунке изображены график функции  . Найдите значение производной функции
. Найдите значение производной функции  на отрезке
на отрезке  .
.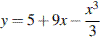 на отрезке
на отрезке  .
. на отрезке
на отрезке  .
.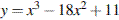 на отрезке
на отрезке  .
.

 В первом банке один австралийский доллар можно купить за 28,6 рубля. Во втором банке 120 долларов — за 3420 рублей. В третьем банке 40 долларов стоят 1148 рублей. Какую наименьшую сумму (в рублях) придется заплатить за 30 австралийских долларов?
В первом банке один австралийский доллар можно купить за 28,6 рубля. Во втором банке 120 долларов — за 3420 рублей. В третьем банке 40 долларов стоят 1148 рублей. Какую наименьшую сумму (в рублях) придется заплатить за 30 австралийских долларов? равны 6 и 8. Диагонали пересекаются в точке
равны 6 и 8. Диагонали пересекаются в точке  . Найдите длину суммы векторов
. Найдите длину суммы векторов  и
и  .
. . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
. Если уравнение имеет более одного корня, в ответе запишите меньший из корней. Большее основание равнобедренной трапеции равно 34. Боковаяясторона равна 14. Синус острого угла равен
Большее основание равнобедренной трапеции равно 34. Боковаяясторона равна 14. Синус острого угла равен  . Найдите меньшее основание.
. Найдите меньшее основание.
 Найдите площадь поверхности многогранника изображенного на рисунке (все двугранные углы прямые).
Найдите площадь поверхности многогранника изображенного на рисунке (все двугранные углы прямые). .
. , где
, где 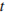 — время в минутах,
— время в минутах,  мин — начальная угловая скорость вращения катушки, а
мин — начальная угловая скорость вращения катушки, а  мин
мин  — угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки
— угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки  достигнет 4050°. Определите время после начала работы лебeдки, не позже которого рабочий должен проверить еe работу. Ответ выразите в минутах.
достигнет 4050°. Определите время после начала работы лебeдки, не позже которого рабочий должен проверить еe работу. Ответ выразите в минутах.
 на отрезке
на отрезке  .
.


