Решение Райсснера — Нордстрёма
Это статичное решение (не зависящее от временной координаты) уравнений Эйнштейна для сферически-симметричной чёрной дыры с зарядом, но без вращения. Метрика чёрной дыры Райсснера — Нордстрёма:
где c — скорость света, м/с, t — временная координата (время, измеряемое на бесконечно удалённых неподвижных часах), в секундах, r — радиальная координата (длина «экватора» изометрической сферы[Комм 3], делённая на θ — полярная угловая координата, в радианах, φ — азимутальная угловая координата, в радианах,
где Параметры чёрной дыры не могут быть произвольными. Максимальный заряд, который может иметь ЧД Райсснера — Нордстрёма, равен Это решение, при продолжении за горизонт, аналогично шварцшильдовскому, порождает удивительную геометрию пространства-времени, в которой через чёрные дыры соединяется бесконечное количество «вселенных», в которые можно попадать последовательно через погружения в чёрную дыру.
|


 ), в метрах,
), в метрах,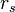 — радиус Шварцшильда (в метрах) тела с массой M,
— радиус Шварцшильда (в метрах) тела с массой M, — масштаб длины (в метрах), соответствующий электрическому заряду Q (аналог радиуса Шварцшильда, только не для массы, а для заряда) определяемый как
— масштаб длины (в метрах), соответствующий электрическому заряду Q (аналог радиуса Шварцшильда, только не для массы, а для заряда) определяемый как
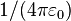 — постоянная Кулона.
— постоянная Кулона. где e — заряд электрона. Это частный случай ограничения Керра — Ньюмена для ЧД с нулевым угловым моментом (
где e — заряд электрона. Это частный случай ограничения Керра — Ньюмена для ЧД с нулевым угловым моментом ( то есть без вращения). При превышении этого критического заряда формально решение уравнений Эйнштейна существует, но «собрать» такое решение из внешнего заряженного вещества не получится: гравитационное притяжение не сможет компенсировать собственное электрическое отталкивание материи (см.: Принцип космической цензуры). Кроме того, надо заметить, что в реалистичных ситуациях чёрные дыры не должны быть сколь-либо значительно заряжены.
то есть без вращения). При превышении этого критического заряда формально решение уравнений Эйнштейна существует, но «собрать» такое решение из внешнего заряженного вещества не получится: гравитационное притяжение не сможет компенсировать собственное электрическое отталкивание материи (см.: Принцип космической цензуры). Кроме того, надо заметить, что в реалистичных ситуациях чёрные дыры не должны быть сколь-либо значительно заряжены.


