II способ.
РАЗДЕЛ 2 СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ Основные понятия и теоремы Постановка задачи. Требуется найти значения х 1, х 2, …, хn удовлетворяющие следующим соотношением:
Используя эти обозначения, можно систему записать в матричной форме: Ах = b. Если b 1 = b 2 = ¼= bm = 0, то система уравнений называется однородной. Если хотя бы одно из bk (k = 1, 2, ¼, m) отлично от нуля, то система называется неоднородной.
Матрица Если система имеет хотя бы одно решение, то она называется совместной. При этом система, имеющая единственное решение называется определенной, а более одного решения – неопределенной. Если система не имеет решений, то она называется несовместной. При решении систем линейных уравнений предстоит ответить на три вопроса: А. Совместна ли система? В. Определена ли система? С. Как найти решение (или решения) системы. Правило Крамера. Если система уравнений невырождена (т.е. det A ¹ 0), то система определена, т.е. имеет единственное решение, и ее решение может быть найдено по формулам Крамера: Ранг матрицы. С решением систем непосредственно связано понятие ранга матрицы. Ранг матрицы – это наивысшей порядок ее минора, отличного от нуля. При нахождении ранга матрицы важно ориентироваться в том, какие преобразования с матрицей можно делать, не изменяя при этом ее ранг: 1°. транспонирование; 2°. перестановка двух строк (столбцов); 3°. умножение всех элементов строки (или столбца) на число с ¹ 0; 4°. прибавление ко всем элементам строки (столбца) соответствующих элементов другой строки (столбца); 5°. выбрасывание нулевой строки (столбца); 6°. вычеркивание строки (столбца), являющейся линейной комбинацией остальных строк (столбцов). Однородные системы. Рассматривается однородная система линейных уравнений с n неизвестными: Ах = 0. Если rang A = n (det A ¹ 0), то система определена и имеет только тривиальное решение: x 1 = x 2 = … = xn = 0. Если rang A < n (det A = 0), то система имеет и не тривиальные решения. При этом все решения однородной системы уравнений образуют линейное пространство L и dim L = n – rang A. Чтобы найти базис пространства решений однородной системы уравнений поступают так: 1. Находят базисный минор матрицы А; 2. Если строка не входит в базисный минор, то соответствующие ей уравнение является линейной комбинацией остальных уравнений и его можно выбросить. 3. Если столбец не входит в базисный минор, то неизвестная с соответствующим номером назначается свободной. Всего найдется (n – rang A) свободных неизвестных. 4. Пусть свободные неизвестные хr +1, хr +2, …, хn. Если дать свободным неизвестным произвольные значения, то получим систему относительно хr +1, хr +2, …, хn у которой определитель не равен нулю и, следовательно, система имеет единственное решение. 5. Дадим свободным неизвестным значения (1, 0, 0, 0, …, 0), затем (0, 1, 0, 0, …, 0) и т.д. Решая, получившиеся системы, получим соответственно векторы 6. Общее решение линейной системы однородных уравнений в этом случае есть линейная комбинация базисных векторов:
Неоднородные системы. Теорема Кронекера – Капелли: Система неоднородных линейных уравнений Ах = b совместна тогда и только тогда, когда rang A = rang Ã. При этом, если rang A = rang à = n, то система имеет единственное решение, и оно может быть найдено по правилу Крамера. Если rang A = rang à < n, то система имеет бесконечно много решений, которые образуют линейное многообразие. При этом, сдвигаемое подпространство – это пространство L решений однородной системы уравнений и его базис может быть построен, как уже было указано выше. Вектор сдвига – это частное решение неоднородной системы уравнений и он может быть найден, если в неоднородной системе свободные неизвестные положить равными некоторым произвольным значениям (например, нулевым). Общее решение неоднородной системы – есть общее решение соответствующей однородной системы плюс некоторое частное решение неоднородной системы. Последнее утверждение можно записать через аббревиатуры соответствующих терминов: О.Р.Н.С. = О.Р.О.С. + Ч.Р.Н.С. Обратная матрица. Запишем систему в матричном виде Ах = b. Если det A ¹ 0 (такая матрица А называется невырожденной), то для матрицы А существует матрица А –1 такая, что А –1 А = АА –1 = Е и тогда решение системы может быть записано в виде: А –1 Ах = А –1 b Þ х = А –1 b. Таким образом, в случае существования обратной матрицы А –1решение системы пишется в виде х = А –1 b. Как же найти обратную матрицу А –1 к невырожденной матрице А? I способ. 1) Составим матрицу Аik из алгебраических дополнений к элементам аik матрицы А; 2) Транспонируем матрицу из алгебраических дополнений; 3) Каждый элемент получившейся матрицы делим на det A. Получившаяся матрица – А –1. II способ. 1) Запишем матрицу А, а справа от нее, через вертикальную черту, запишем единичную матрицу. Получим матрицу n – строк, 2 n – столбцов; 2) В получившейся матрице с помощью применения к строкам (и только) преобразований не изменяющих ранг матрицы образуем на месте матрицы А – единичную матрицу. На месте единичной матрицы стоит А –1. III способ. Справа от матрицы припишем единичную матрицу Е, а снизу припишем матрицу (– Е). В правом нижнем углу поставим нулевую матрицу. Используя операции только над строками, получившейся матрицы, на месте матрицы (– Е), образуем нулевую матрицу. Тогда, в правом нижнем углу будет стоять А –1. IV способ. Для обращения матрицы, имеющей блочную структуру, т.е. матрицы вида: 1. Первая формула Фробениуса (если det A ¹ 0):
2. Вторая формула Фробениуса (если det D ¹ 0):
Контрольные вопросы и задания
1. Что такое ранг матрицы и ее базисный минор? Определяются ли они однозначно? 2. Найти ранг и все базисные миноры матрицы: 3. Как связаны ранг матрицы и размерность линейной оболочки ее строк. 4. Чему равна размерность пространства решений однородной системы линейных уравнений, если в системе: 10 уравнений, 16 неизвестных и ранг матрицы системы равен 6? 5. Образует ли множество решений неоднородной системы линейное пространство? Какое из свойств линейного пространства не выполнено? 6. Вспомните определение линейного многообразия. Что называется его базисом и размерностью? 7. Как определяется вектор сдвига для линейного многообразия, являющегося множеством решений неоднородной системы?
|

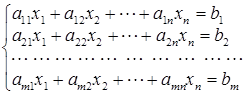 здесь aij (i = 1, 2, …, m; j = 1, 2, …, n) и bk (k = 1, 2, …, m) – заданные числа.
здесь aij (i = 1, 2, …, m; j = 1, 2, …, n) и bk (k = 1, 2, …, m) – заданные числа.
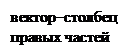
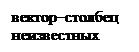
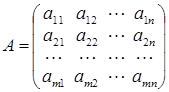 ;
; 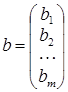 ;
; 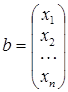
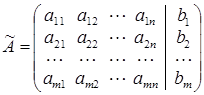 .
.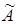 называется расширенной матрицей системы.
называется расширенной матрицей системы.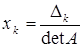 (k = 1, 2, …, n) где D k – определитель матрицы, которая получится, если в матрице А системы k -й столбец заменить на столбец свободных членов.
(k = 1, 2, …, n) где D k – определитель матрицы, которая получится, если в матрице А системы k -й столбец заменить на столбец свободных членов. . Эти векторы и образуют базис пространства L решений однородной системы линейных уравнений.
. Эти векторы и образуют базис пространства L решений однородной системы линейных уравнений.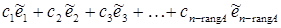 .
.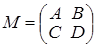 , где А – квадратная матрица порядка n ´ n, а D – квадратная матрица q ´ q, справедливы следующие формулы:
, где А – квадратная матрица порядка n ´ n, а D – квадратная матрица q ´ q, справедливы следующие формулы: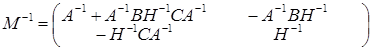 , где H = D – CA –1 B.
, где H = D – CA –1 B.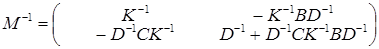 , где K = A – BD –1 C.
, где K = A – BD –1 C.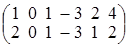 .
.


