Примеры решения задач. Задача 1. Найти ранг матрицы .
Задача 1. Найти ранг матрицы Решение. Прежде всего, отметим, что четвертая строка матрицы есть сумма второй и третьей строк и поэтому при отбрасывании этой строки ранг матрицы не изменится. 1. Отбросим четвертую строку; 2. Из второй и третьей строк матрицы вычтем первую строку, умноженную, соответственно, на 2 и 3; 3. В полученной матрице из третьей строки вычтем вторую, умноженную на 2. Получим цепочку преобразований:
В полученной матрице, минор, стоящий в первых, трех столбцах отличен от нуля. Следовательно, ранг исходной матрицы равен трем и минор 3го порядка, стоящий в первых, трех столбцах есть базисный минор матрицы А. Задача 2. Найти матрицу обратную к матрице Решение. Пусть обратная матрица имеет вид: Перемножая матрицы, получим равенства:
из этих соотношений получаем: g = 0, d = 0, a = 1; далее: h = 0, e =1, b = –3. И наконец: m = 1, f = –2, c = 11. В итоге приходим к выводу, что:
Задача 3. Найти матрицу обратную к матрице Решение. Построим матрицу 6 ´ 6 приписав справа от А единичную матрицу Е, а внизу матрицу (– Е), остальные места заполним нулями.
С помощью операций над строками матрицы А ¢ образуем на месте (– Е) нулевую матрицу. Тогда в правом нижнем углу будет стоять матрица А –1. 1. Ко всем строкам матрицы А –1 прибавим третью строку с некоторым множителем, добиваясь того, чтобы все элементы первого столбца, кроме а 31, равнялись нулю. 2. Первую строку полученной матрицы разделим на (–3) и, прибавляя к остальным строкам матрицы полученную первую строку с некоторыми множителями, добьемся того, чтобы во втором столбце стояли нули, кроме элемента а 12. 3. С помощью второй строки образуем нули в третьем столбце, кроме элемента а 23. Получим цепочку преобразований:
Задача 4. Найти матрицу обратную к Решение. Для обращения матрицы применим первую формулу Фробениуса. Полагаем: Находим последовательно:
И тогда Задача 5. С помощью правила Крамера решить систему линейных неоднородных уравнений: Решение. Главная матрица системы имеет вид: Так как det A = D = 18 ¹ 0, то решение системы может быть найдено по правилу Крамера. Для этого составим определители D х, D у, D z, которые отличаются от главного определителя тем, что в нем столбец коэффициентов при х, у и z соответственно, заменен на столбец свободных членов, т.е.:
Вычисляя их, находим, что D х = 18, D у = 36, D z = 54. И тогда Задача 6. Решить систему линейных однородных уравнений:
Решение. Прежде всего, отметим, что система наверняка совместна, ибо однородная система всегда имеет по меньшей мере нулевое решение. Займемся нахождением общего решения данной системы. Главная матрица системы имеет вид: Найдем ранг матрицы А. Первую строку матрицы с соответствующими множителями прибавим к остальным строкам матрицы так, чтобы первый столбец обратился в ноль, кроме элемента а 11. Получится матрица А 1 такая, что rang A 1 = rang A и Тогда получилась система двух уравнений, из которых можно написать: х 1 = 14 х 3 – 7 х 4 + 3 х 5 – х 6, х 2 = –7 х 3 + 2 х 4 – х 5 – 2 х 6 и переменные х 3, х 4, х 5, х 6 – любые. Это и есть решение системы. Однако, можно (и должно) пойти дальше. Множество решений линейной однородной системы образует линейное пространство L размерности dim L = n – rang A = 6 – 2 = 4. Для нахождения базисных векторов пространства решений дадим свободным неизвестным х 3, х 4, х 5, х 6 значения: а) 1, 0, 0, 0; б) 0, 1, 0, 0; в) 0, 0, 1, 0; г) 0, 0, 0, 1. Получим четыре вектора, образующие базис L: е 1 = (14, –7, 1, 0, 0, 0); е 2 = (–7, 2, 0, 1, 0, 0); е 3 = (3, –1, 0, 0, 1, 0); е 4 = (–1, –2, 0, 0, 0, 1). Таким образом: L = ℒ(е 1, е 2, е 3, е 4) и любое решение исходной системы может быть записано в виде линейной комбинации базисных векторов, т.е. в виде: с 1(14, – 7, 1, 0, 0, 0) + с 2(– 7, 2, 0, 1, 0, 0) + + с 3(3, –1, 0, 0, 1, 0) + с 4(–1, –2, 0, 0, 0, 1), где с 1, с 2, с 3, с 4 – любые значения. Это и есть общее решение исходной линейной однородной системы уравнений. Задача 7. Решить систему линейных неоднородных уравнений
Решение. Расширенная матрица системы уравнений имеет вид: Это и есть общее решение исходной системы уравнений. Однако, с целью прояснить алгебраическую структуру решения системы, мы отметим следующее: Так как rang Отсюда: х 1 = 14 х 3 – 7 х 4 – 3 х 5, х 2 = – 7 х 3 + 2 х 4 – х 5, где х 3, х 4, х 5 – любые. Давая свободным переменным х 3, х 4, х 5 значения: а) 1, 0, 0; б) 0,1,0; в) 0, 0, 1 получим, соответственно, базисные векторы пространства L решений однородной системы уравнений: е 1 = (14, –7, 1, 0, 0), е 2 = (–7, 2, 0, 1, 0), е 3 = (–3, –1, 0, 0, 1). Тогда решения исходной системы образуют линейное многообразие М: M = { x ½ x = f + c 1 e 1 + c2e2 + c 3 e 3}, где с 1, с 2, с 3 – любые. Итак, любое решение неоднородной системы уравнений представимо в виде: (1, 2, 0, 0, 0) + с 1(14, –7, 1, 0, 0) + с 2(–7, 2, 0, 1, 0) + с 3(3, –1, 0, 0, 1).
|

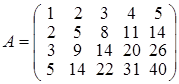 .
.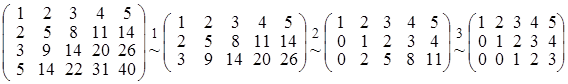 .
.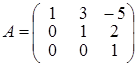 .
.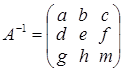 . Тогда, по определению: АА –1 = Е, т.е.
. Тогда, по определению: АА –1 = Е, т.е. 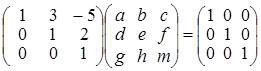 .
.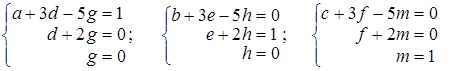 ,
,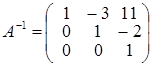 .
. .
.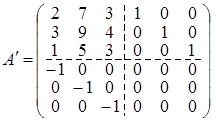 .
.
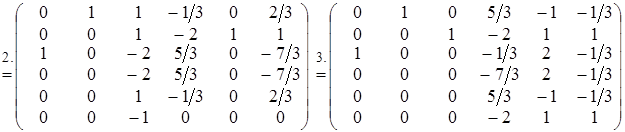 Отсюда заключаем, что
Отсюда заключаем, что 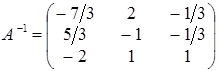 .
.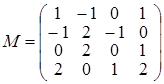 .
.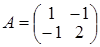 ,
, 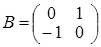 ,
,  ,
,  .
. ;
;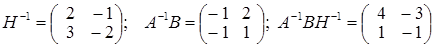 ;
;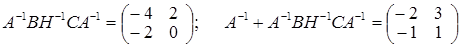 ;
; .
.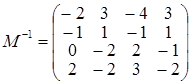 . Привлекательность указанного способа состоит в том, что для обращения матрицы 4го порядка мы имеем дело с обращением матриц лишь 2го порядка, что существенно проще.
. Привлекательность указанного способа состоит в том, что для обращения матрицы 4го порядка мы имеем дело с обращением матриц лишь 2го порядка, что существенно проще.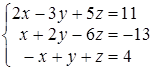 .
.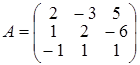 .
.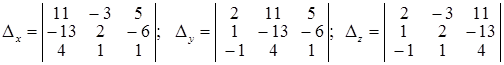 .
.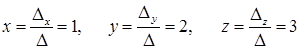 .
. .
.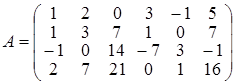 .
.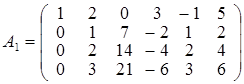 . Отмечая, что третья и четвертая строка матрицы пропорциональны второй строке, заключаем, что rang A 1 = rang A 2, где
. Отмечая, что третья и четвертая строка матрицы пропорциональны второй строке, заключаем, что rang A 1 = rang A 2, где 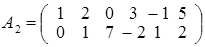 , умножим вторую строку матрицы А 2 на (–2) и прибавим к первой строке. Получим матрицу А3:
, умножим вторую строку матрицы А 2 на (–2) и прибавим к первой строке. Получим матрицу А3: 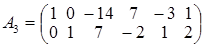 , такую что rang A 3 = rang A 2 = 2. В итоге rang A = rang A 3 = 2.
, такую что rang A 3 = rang A 2 = 2. В итоге rang A = rang A 3 = 2.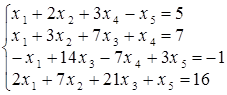 .
.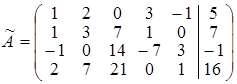 , причем, до вертикальной черты, записана матрица системы, а после вертикальной черты – столбец свободных членов. Преобразовывая матрицу
, причем, до вертикальной черты, записана матрица системы, а после вертикальной черты – столбец свободных членов. Преобразовывая матрицу 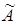 , аналогично тому, как преобразовывалась матрица А в решении предыдущей задачи, получим матрицу А 1, такую, что rang
, аналогично тому, как преобразовывалась матрица А в решении предыдущей задачи, получим матрицу А 1, такую, что rang  . Отсюда можно написать общее решение системы в виде: х 1 = 1 + 14 х 3 – 7 х 4 – 3 х 5, х 2 = 2 – 7 х 3 + 2 х 4 – х 5, где х 3, х 4, х 5 – любые.
. Отсюда можно написать общее решение системы в виде: х 1 = 1 + 14 х 3 – 7 х 4 – 3 х 5, х 2 = 2 – 7 х 3 + 2 х 4 – х 5, где х 3, х 4, х 5 – любые.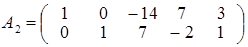 .
.


