Задачи и упражнения для самостоятельной работы
1. Найти ранг матриц: а)
2. Найти ранг матриц: а)
3. Найти ранги следующих матриц: а) д)
4. Найти ранги следующих матриц в зависимости от значений параметра: а)
2 для w = 0 и w = –2; 3 для остальных w; г) 2 для l =3; 3 для остальных l.
5. Найти матрицы обратные к заданной: а) г) D а) д)
6. Найти матрицы обратные к заданной: а) в) D а)
7. Решить матричные уравнения: а) в) D а) 8. Решить матричные уравнения: а) в) D а)
9. Решить следующие матричные уравнения: а) в) D а)
10. Решить следующие матричные уравнения: а) в) D а)
11. Решить системы уравнений: а) в)
12. Решить системы уравнений (немного наблюдательности): а) в)
13. Решить системы уравнений по правилу Крамера: а) в)
14. Решить системы уравнений: а) в)
15. Решить системы линейных однородных уравнений: а) х – у = 0; б) х 1 – х2 +2 х 3 = 0; в) х 1 + х 2 + х 3 + х 4 + х 5 = 0.
16. Решить системы линейных однородных уравнений: а) в)
17. Решить системы линейных однородных уравнений: а) в) д)
г) (h 1, h 1 + h 2, h 2, – 2 h 1, – h 2); д) (h 1, h 1 + h 2, h 2, – 2 h 1, – h 2).
18. Найти базис и размерность пространства решений (фундаментальное решение) системы линейных однородных уравнений и выписать общее решение: а) в)
+ с 3(0, –1, 0, 0, 0, 1)
19. Решить системы линейных уравнений методом исключения неизвестных: а) в)
х 1 и х 2 можно выразить через х 3 и х 4: х 1 = 6 – 26 х 3 + 17 х 4; х 2 = –1 + 7 х 3 – 5 х 4.
20. Решить системы методом исключения неизвестных: а) в)
21. Решить неоднородные системы линейных уравнений: а) в) D а) (2, 0) + с (3, 2); б) (1, 0, 0, 0) + с 1(–1, 1, 0, 0) + с 2(–2, 0, 1, 0) + с 3(–3, 0, 0, 1); в) (0, 0, 4) + + с (1, 1, – 3); г) (6, 8, 0, 0, 0) + с 1(–1, –1, 1, 0, 0) + с 2(–1, –1, 0,1,0) + с 3(–1, –1, 0, 0, 1).
22. Исследовать на совместность и решить системы: а) в) D а) (3, 2, 1); б) (1, 1, 1, –1) + с 1(1, 0, –15, 18) + с 2(0, 1, 10, –12); в) (2, 1, 22/5, 8/5) + + с 1(5, 0, 34, 16) + с 2(0, 5, –17, –8); г) (1, 1, 8/13, –11/13) + с 1(13, 0, –27, 3) + с 2(0, 13, 9, –1).
23. Исследовать системы на совместность и, в случае совместности, решить их: а) в) D а) (–1, 1, 0, 1) + с 1(1, –5, 11, 0) + с 2(–9, 1, 0, 11); б) (2, 1, 0, 0) + с 1(1, 0, 22, –16) + + с 2(0, 1, –33, 24); в) (–1, 1, 0, 1) + с 1(1, 0, –3, 0) + с 2(0, 1, –4, 0); г) система не совместна.
24. Решить неоднородные системы уравнений: а) в) D а) (1 – h 1, – h 2, 1 + h 1 + 2 h 2, –1 + 2 h 1 + 3 h 2); б) (–1 – 5 h, 6 h, –1 – 5 h, 1 + 7 h); в) (2 +4 h 1 –11 h 2 –14 h 3, 1–22 h 1+32 h 2 +23 h 3, –1+3 h 1, –1+15 h 2, –1+15 h 3); г) (–2– h,– h, 2+ h, 1).
25. Исследовать системы и найти общее решение в зависимости от l: а) в) D а) l ¹ 5 – нет решений; l = 5: – нет решений; l = 1: х 1 = 1 – х 2 – х 3; l ¹ 1 и l ¹ –2: в) Если l ¹ 1 и l ¹ –2 – единственное решение х 1 = 1 – х 2 – х 3 (х 2, х 3 – любые); если l = –2 – нет решений; г) Если l ¹ 0 и l ¹ –3 – единственное решение: l = –3 система не совместна.
26. Решить системы линейных уравнений с заданными расширенными матрицами: а) в) D а) х 3, х 4 – любые; в) х 2 = 2 – х 3 + 2 х 4, х 3, х 4 – любые.
27. Решить системы линейных уравнений с заданными расширенными матрицами: а) в) д) D а) х 1 = 1 + х 3 – х 4, х 2 = 2 – х 3 + 2 х 4, х 3, х 4 – любые; б) х 1 = –11 + 11 х 3 + 5 х 4, х 2 = 4 – 2 х 3 – х 4, х 3, х 4 – любые; в) х 1 = 1 – 3 х 3 + х 4, х 2 = 1 – 4 х 3 + 2 х 4, х 3, х 4 – любые; г) е) х 1 = –1 – 3 х 3 + 3 х 4, х 2 = 1 + х 3 – 2 х 4, х 3, х 4 – любые.
ЛИТЕРАТУРА
1. Курош А.Г. Курс высшей алгебры. – М.: Наука, 1975. 2. Гельфанд И.М. Лекции по линейной алгебре. – М.: Наука, 1971. 3. Мальцев А.И. Основы линейной алгебры. – М.: Наука, 1970. 4. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, 1973. 5. Шилов Г.Е. Математический анализ. Конечномерные линейные пространства. – М.: Наука, 1969. 6. Головина Л.И. Линейная алгебра и некоторые ее приложения. – М.: Наука, 1985. 7. Бутузов В.Ф., Крутицкая Н.Ч., Шишкин А.А. Линейная алгебра в вопросах и задачах. – М.: Физматлит, 2001. 8. Проскуряков И.В. Сборник задач пол линейной алгебре. – М.: Наука, 1974.
|

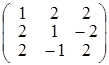 ; б)
; б)  ; в)
; в) 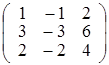 ; г)
; г)  .
.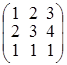 ; б)
; б) 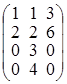 ; в)
; в)  ; г)
; г) 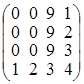 .
.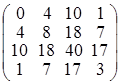 ; б)
; б)  ; в)
; в)  ; г)
; г) 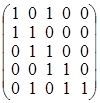 ;
;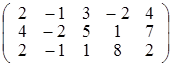 ; е)
; е)  .
.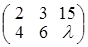 ; б)
; б) 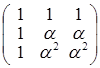 ; в)
; в) 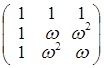 ; г)
; г) 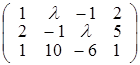 .
.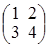 ; б)
; б) 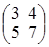 ; в)
; в) 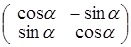 ;
; ; д)
; д) 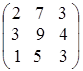 ; е)
; е) 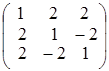 .
.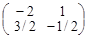 ; б)
; б)  ; в)
; в) 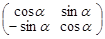 ; г)
; г) 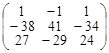 ;
; ; е)
; е) 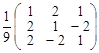 .
. 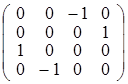 ; б)
; б) 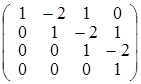 ;
;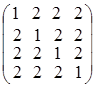 ; г)
; г) 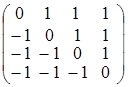 .
. ; б)
; б)  ; в)
; в) 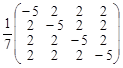 ; г)
; г)  .
. 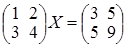 ; б)
; б)  ;
;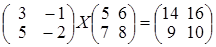 ; г)
; г) 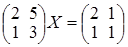 .
.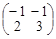 ; б)
; б)  ; в)
; в) 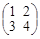 ; г)
; г) 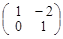 .
. 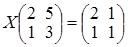 ; б)
; б) 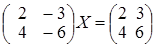 ;
;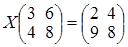 ; г)
; г)  .
. ; б)
; б)  ; в)
; в) 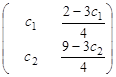 ; г) нет решений.
; г) нет решений.  ; б)
; б)  ;
;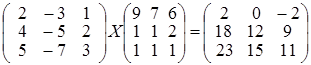 ; г)
; г) 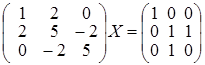 .
. ; б)
; б) 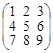 ; в)
; в) 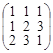 ; г)
; г) 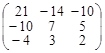 .
.  ; б)
; б) 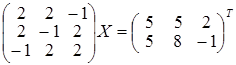 ;
; ; г)
; г)  .
. ; б)
; б) 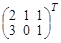 ; в)
; в)  ; г)
; г) 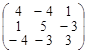 .
. 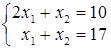 ; б)
; б)  ;
;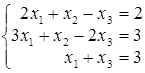 ; г)
; г)  .
. ; б)
; б) 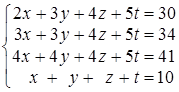 ;
; ; г)
; г)  .
.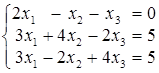 ; б)
; б) 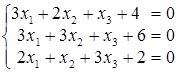 ;
;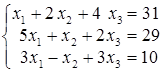 ; г)
; г)  .
.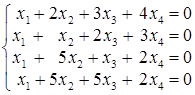 ; б)
; б) 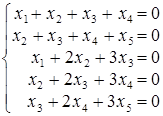 ;
;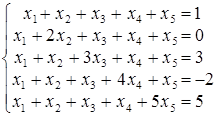 ; г)
; г) 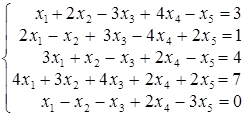 .
.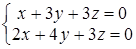 ; б)
; б)  ;
;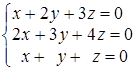 ; г)
; г)  .
.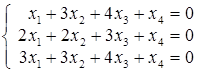 ; б)
; б)  ;
; ; г)
; г)  ;
;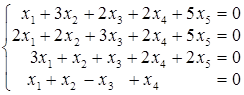 .
.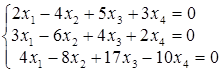 ; б)
; б) 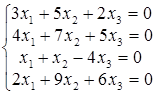 ;
;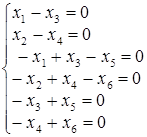 ; г)
; г)  .
.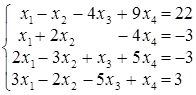 ; б)
; б)  ;
;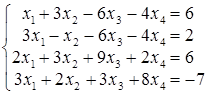 ; г)
; г) 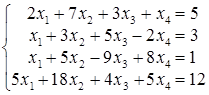 .
. ; б)
; б) 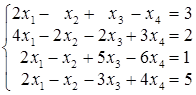 ;
;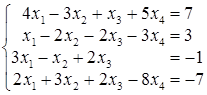 ; г)
; г) 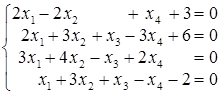 .
.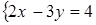 ; б)
; б) 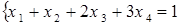 ;
;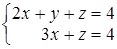 ; г)
; г)  .
.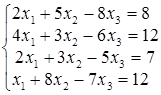 ; б)
; б) 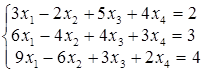 ;
;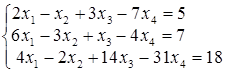 ; г)
; г) 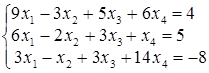 .
. ; б)
; б)  ;
;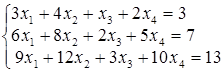 ; г)
; г) 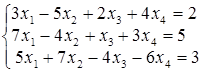 .
.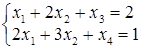 ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б) 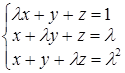 ;
; ; г)
; г)  .
.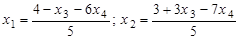 , х 3, х 4 – любые; б) l = –2
, х 3, х 4 – любые; б) l = –2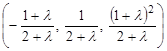 ;
;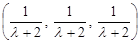 ; если l = 1:
; если l = 1: ; l = 0 или
; l = 0 или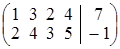 ; б)
; б) 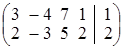 ;
;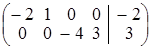 ; г)
; г)  .
. , х 3, х 4 – любые; б) х 1 = –5– х 3+5 х 4, х 2 = – 4 + х 3 +4 х 4,
, х 3, х 4 – любые; б) х 1 = –5– х 3+5 х 4, х 2 = – 4 + х 3 +4 х 4, , х 2 = 2 х 1– 2, х 3, х 1 – любые; г) х 1 = 1 + х 3 – х 4,
, х 2 = 2 х 1– 2, х 3, х 1 – любые; г) х 1 = 1 + х 3 – х 4,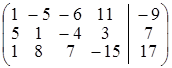 ; б)
; б) 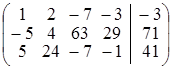 ;
; ; г)
; г)  ;
; ; е)
; е)  .
.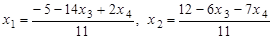 , х 3, х 1 – любые; д) (8, –5, 10, –5);
, х 3, х 1 – любые; д) (8, –5, 10, –5);


