Системы счисления. Мы не будем здесь учиться программировать или складывать двоичные числа в столбик

Мы не будем здесь учиться программировать или складывать двоичные числа в столбик. Первое музыканту не обязательно, а второе проще делать на калькуляторе.

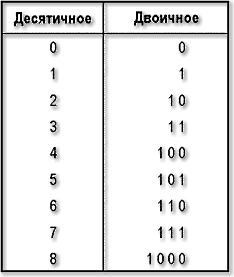
На самом деле, чтобы разобраться в протоколе MIDI, вовсе необязательно иметь математический склад ума. Нужно только базовое представление о способе хранения чисел в компьютере. Если однажды в секвенсоре вы увидели окно SysEx с кучей непонятных букв и цифр, и рефлекторно закрыли его, то этот раздел для вас. Попробуйте изменить свое отношение к этим значкам, а еще лучше — почитайте руководство пользователя к инструменту и попробуйте эти значки на практике. Вы увидите, что они обладают огромной силой.

Как же хранится информация в цифровых устройствах? Логично предположить, что раз "цифровые", то в виде привычных для нас чисел. Люди используют десятичную систему счисления, возникшую благодаря пальцевому счету — числу пальцев на обеих руках. У нас есть десять различных знаков (цифр), с помощью которых мы можем представить любое число. Если бы у нас было по три пальца на каждой руке (какой ужас), мы бы наверняка пользовались шестеричной системой счисления. И выражали бы любые числа, используя шесть цифр — 0, 1, 2, 3, 4, 5.

У цифрового устройства пальцев нет совсем, а есть только электрические элементы, которые могут находиться либо во включенном, либо в выключенном состоянии. Можно представлять себе такой элемент в виде конденсатора, который либо заряжен, либо разряжен. Программисты договорились, что одно состояние конденсатора будет обозначаться цифрой 0, а другое — 1. Могли бы использовать буквы A и B, суть от этого не изменилась бы. Итак, на все нам даны две цифры, и поэтому система счисления в цифровой технике — двоичная. Цифры в двоичной системе обычно называют битами (от англ. bit — binary digit). Также битом называют простейшую, неделимую область памяти (тот самый конденсатор), в котором хранится какая-либо из цифр двоичной системы. По сути, бит — это минимальная единица информации. Не стоит путать этот "бит" с музыкальным термином, звучащим по-русски аналогично, но обозначающим "удар" (от англ. beat).

Итак, бит принимает только два значения — обычно 0 и 1, хотя эти цифры условны. Например, бит может показывать логическое состояние "да/нет", наличие или отсутствие жесткого диска в семплере, или, скажем, тип дороги — асфальтовая или грунтовая. Понятно, что многие явления двумя состояниями не описать, а числа одним битом не выразить. Для этих целей применяется набор битов. Например, посчитаем в двоичной системе до восьми, и посмотрим, сколько битов (простейших ячеек памяти) нужно для представления чисел (рис. 9):

Нетрудно заметить: максимальное число, которое можно записать, располагая N битами, равно 2N-1. Действительно, двумя битами можно выражать числа до 3, тремя до 7 и так далее.

Для удобства доступа к данным в цифровой технике биты объединяются в группы. Самая распространенная и всем знакомая группа битов — байт. Байт состоит из восьми битов. Биты нумеруются справа налево — нулевой бит всегда находится справа и называется младшим значащим разрядом (LSD, Least Sign­ificant Digit). Самый левый бит называется старшим значащим разрядом (MSD, Most Significant Digit), рис. 10. Получается, что в одном восьмибитовом байте могут храниться значения от 0 до 255 (28-1), то есть всего 256 значений. Если нужно хранить числа больше 255, используются два байта (машинное слово, 16 бит), диапазон значений от 0 до 216-1 (65535), четыре байта (двойное слово, 32 бита) — от 0 до 232-1 (4294967295), и так далее. Заметьте, что число бит, используемых для хранения числа, всегда кратно восьми. Даже если для представления числа достаточно 9 бит, используются два байта. Группы байт объединяются в соответствии со степенями двойки: 2, 4, 8, 16 и так далее. Так что трехбайтовая величина (24 бита) в памяти машины все равно занимает 4 байта, старшие восемь бит просто не используются. Такое расточительство ресурсов связано с особенностью архитектуры микропроцессоров.

 

В протоколе MIDI значения параметров обычно ограничены двухбайтовым словом. Биты с 0 по 7 составляют младший значащий байт слова (LSB, Least Significant Byte), с 8 по 15 — старший значащий байт (MSB, Most Significant Byte).

Двоичные числа очень громоздки в записи и удобны, пожалуй, только для электронных "мозгов": например, число 35935 в двоичной системе будет выглядеть как 1000110001011111. Перевести такое число в десятичное без калькулятора проблематично, как, впрочем, и получить его из десятичного. Поэтому для облегчения жизни программисты придумали шестнадцатеричную систему счисления. В ней числа представляются с помощью цифр и букв: цифры — привычные для нас, от 0 до 9, а буквы — от A до F. Например, в десятичной системе число "десять" записывается как 10, а в шестнадцатеричной — как A. Значение F соответствует десятичному 15.

Важно понять, что компьютеру абсолютно все равно, как мы там называем числа — цифрами, буквами или точками с тире. На физическом уровне есть только электрические элементы, способные находиться в одном из двух состояний. А то, что в компьютерном мире и, в частности, в протоколе MIDI используются именно шестнадцатеричные числа, вызвано удобством их перевода в двоичные, то есть на язык компьютера, и обратно.

В самом деле, максимальное число, которое можно представить одним шестнадцатеричным знаком (F, десятичное 15), равно максимальному числу, которое можно представить четырьмя битами (24-1). Максимальное число, которое можно представить двумя шестнадцатеричными знаками (FF, десятичное 255), равно числу, которое можно представить восемью битами (28-1). И так далее. Получается, что каждые четыре бита двоичного числа соответствуют одному разряду шестнадцатеричного (24 = 16). Следующая таблица (рис. 11) показывает соответствие между двоичными, десятичными и шестнадцатеричными числами.

С помощью нее можно быстро, без калькулятора, выполнять преобразование двоичных чисел в шестнадцатеричные и обратно. Работая с MIDI даже на уровне пользователя, такие преобразования иногда приходиться выполнять. Например, преобразуем наше число 35935 из двоичного вида (1000110001011111) в шестнадцатеричный. Первая четырехбитная группа справа — 1111, соответствует шестнадцатеричному F. Вторая группа (0101) — 5, третья (1100) — С, последняя (1000) — 8. Итак, десятичное 35935 в шестнадцатеричном виде выглядит как 8C5F. Аналогично, число D7 записывается в двоичном виде как 11010111.

Преобразования двоичных и шестнадцатеричных чисел в десятичные и обратно проще выполнять на калькуляторе.

Для того, чтобы отличать в тексте шестнадцатеричные числа от десятичных, используются разные методы. Я буду использовать синтаксис языка программирования Си и обозначать шестнадцатеричные числа префиксом "0x". В нашем примере 35935 = 1000110001011111 = 0x8C5F.

Принцип кодирования сообщений
Очевидно, сообщение должно состоять из двух компонентов: первый описывает тип сообщения, то есть отвечает на вопрос "что надо делать", второй — уточняет действие и отвечает на вопрос "как надо делать". Например, при нажатии клавиши первый компонент сообщает тон-генератору "взять ноту", а второй уточняет: "Эта нота — До малой октавы". В некоторых случаях уточняющий компонент не нужен, например, в системном сообщении реального времени, останавливающем секвенсор, достаточно одного компонента, который говорит "стоп".

Компоненты сообщений в протоколе MIDI представлены байтами. Компонент, описывающий тип сообщения, называется статус-байтом, компонент, уточняющий сообщение — байтом данных. Если уточняющей информации много, она может быть представлена несколькими байтами данных. Таким образом, каждое MIDI-сообщение состоит из одного статус-байта и, если необходимо, одного или нескольких байтов данных. Передаются эти сообщения по MIDI-кабелю в том же порядке — сначала статус-байт, затем байты данных. Количество байтов данных жестко закреплено за каждым сообщением. Так что, если, например, тон-генератор получил статус-байт "нажата клавиша", он ждет за ним два байта данных, первый из которых содержит номер нажатой клавиши, второй — скорость нажатия.

Для системных эксклюзивных сообщений сделано исключение — их длина жестко не задается. Она определяется специальным статус-байтом, который помещается в конец сообщения.

MIDI-сообщения — это поток данных в реальном времени. При передаче данных иногда могут происходить их потери и прочие неприятности. В компьютерных сетевых протоколах, в случае прихода испорченных данных (что проверяется по контрольной сумме) происходит повторный запрос к серверу до тех пор, пока данные не придут в целости и сохранности. В протоколе MIDI такая возможность отсутствует (по крайней мере, при передаче голосовых сообщений), и приемник всегда находится в пассивном состоянии по отношению к передатчику. Что принял, то принял.

Отсюда вывод: необходимо сделать так, чтобы приемник в любой момент мог отличить статус-байт от байта данных, без всяких подсчетов и необходимости синхронизации с передатчиком. Для этого в протоколе MIDI каждый статус байт содержит в старшем значащем разряде единицу, а каждый байт данных — ноль. Так что один бит из байта расходуется по служебной необходимости. Для кодирования сообщений и передачи данных остаются только семь бит. Отсюда — фундаментальное число 128, пронизывающее насквозь весь протокол. Семью битами можно представить только 128 различных значений (от 0 до 127, 27-1). Именно поэтому в MIDI 128 нот, 128 уровней динамики и так далее.

Стало быть, и в статус-байте можно закодировать 128 сообщений. Разработчики протокола могли так и сделать, но поступили иначе, и этим во многом объясняется гибкость и живучесть MIDI. Во-первых, 128 сообщений рано или поздно окажется недостаточно, во-вторых, в каждом сообщении канала нужно передавать номер канала, которому адресовано сообщение. Под номер канала придется отводить один байт данных, что не рационально — сообщения канала используются в MIDI гораздо активнее системных, а если к каждому такому сообщению будет "пришит" дополнительный байт, это намного снизит пропускную способность MIDI. К тому же каналов всего 16, и для их представления достаточно четырех бит. Поэтому было решено кодировать номер канала в младшей половине статус-байта (рис. 12)

Получается такая картина: старший бит статус-байта занят, так как должен всегда содержать единицу, четыре младших байта — тоже, так как содержат номер MIDI-канала. На кодирование типа сообщения остается всего три бита, которыми можно закодировать восемь сообщений. Семь из них отвели под сообщения канала, а последнее, все биты которого единичные (111), сделали признаком системного. Системные сообщения не требуют номера канала, поэтому младшие четыре бита статус-байта могут быть использованы для кодирования конкретного типа сообщения (всего их получается 16).

Тон-генератор анализирует полученный байт примерно по следующей схеме. Если его старший бит равен нулю — это байт данных и младшие семь бит нужно рассматривать как числовой параметр. Если старший бит равен единице — это статус-байт, и тогда три бита после него отражают тип сообщения. Если эти три бита единичные, сообщение системное, какое именно — задается младшими четырьмя битами. В противном случае — это сообщение канала, и тогда младшие четыре бита задают номер канала. Все это может показаться сложным для человека, но компьютер работает с битами "на ура" и вышеуказанную процедуру выполняет за доли микросекунды.

Однако, что же получается: вместо 128 возможных сообщений мы можем закодировать только семь голосовых и шестнадцать системных? Да, именно так. Системных сообщений, в принципе, достаточно, а вот все голосовые в семь штук явно не уложишь. Поэтому разработчики MIDI применили многоуровневый метод кодирования. Но об этом поговорим в следующий раз.

 

2.Сообщения канала

В первой части цикла рассказывалось о предпосылках к появлению MIDI, развитии синтезаторов, о процессе подготовки и внедрения спецификации MIDI, расширении протокола за последние двадцать лет. Рассматривались компоненты MIDI, коммутация устройств, основы двоичной и шестнадцатеричной систем счисления. Начато рассмотрение языка MIDI: типов сообщений и принципов их кодирования.

Мы выяснили, что структура статус-байта MIDI позволяет закодировать семь голосовых и шестнадцать системных сообщений. Возможные варианты наглядно демонстрирует рис. 1.

 

Системные сообщения отложим до лучших времен, а сегодня поговорим о сообщениях канала — основном строительном материале языка MIDI.

Напомню, что сообщения канала делятся на два типа: голосовые и сообщения режима канала. Первые связаны со звукообразованием, вторые к этому прямого отношения не имеют, но играют в деле управления MIDI-устройством не последнюю роль.

Голосовое сообщение заставляет тон-генератор произвести какое-либо изменение в звуке (или, собственно, сам звук). Например, если исполнитель нажимает клавишу, в тон-генератор посылается сообщение Note On, на которое тот реагирует воспроизведением ноты. Если исполнитель поворачивает колесо модуляции, тон-генератор изменяет глубину модуляции звучащей ноты.

Во многих случаях то, каким органом управления создается сообщение, принципиального значения не имеет. Тогда спецификация привязывает сообщение непосредственно к параметру синтеза. Так, для изменения панорамы в MIDI-канале используется сообщение Pan, но спецификация не уточняет, как оно генерируется. То же самое справедливо и в отношении многих других сообщений, например, задающих длительность участков огибающей.

Особое внимание следует обратить на принципиальный момент: в MIDI все параметры синтеза задаются безразмерными числами. Вы поворачиваете колесо модуляции — в тон-генератор приходит сообщение типа "колесо модуляции: 652". Вы нажимаете клавишу — сообщение имеет вид "нота номер 60, динамика взятия 120". Тон-генератор сам решает, как преобразовать эти числа в реальный коэффициент модуляции, в высоту тона в герцах, и в выходной уровень в децибелах.

В некоторых случаях спецификация однозначно задает такое преобразование. Например, нота с номером 60 должна быть всегда нотой До первой октавы и иметь частоту 261 Гц. Тон-генератор подчиняется. В других случаях спецификация рекомендует, чтобы, например, при динамике 120 уровень на выходе осциллятора снижался на 0,98 дБ от максимального. Наконец, для параметров вроде модуляции никаких рекомендаций не дается — коэффициент модуляции зависит от особенностей внутренней архитектуры инструмента.