Указания по выполнению задания
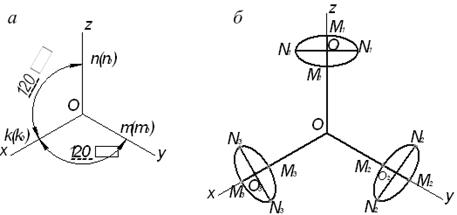
Для выполнения задания нужно мысленно представить предмет в пространстве по его описанию, после чего мысленно построить два отверстия по описанию. В случае затруднений можно вылепить проектируемый предмет из пластилина или вырезать, например, из пенопласта или сделать набросок этого предмета карандашом на бумаге. После того, как будет усвоена конструкция предмета можно приступить к выполнению чертежа. После вычерчивания трех видов внешней формы предмета рекомендуется выполнить на главном виде призматическое отверстие по форме и размерам, приведенным в таблице 6, затем построить проекции этого отверстия на виде сверху и виде слева. После этого следует построить проекции цилиндрического отверстия, начав построение с вида сверху. Построения выполнять тонкими линиями (s/3), применяя штриховые линии для невидимого контура предмета. После построения трех видов нужно выполнить три разреза: горизонтальный, фронтальный и профильный. Правила обозначения и изображения разрезов должны соответствовать ГОСТ 2.305-80. Закончив построение трех изображений предмета, следует нанести размеры в соответствии с ГОСТ 2.307-68. Заключительным этапом является построение наглядного изображения в прямоугольной изометрической проекции, пользуясь приведенными коэффициентами искажения который составляет 0,82. Коэффициент искажения в прямоугольной изометрии вычисляется по формуле k2 + m2 + n2=2, которая при k = m = n приобретает вид: 3k2 = 2, откуда k = 0,82. Как видно, уравнение k2 = m2 = n2=2 при k = m = n имеет только одно решение. А это означает, что существует всего лишь одна прямоугольная изометрия и ей соответствуют коэффициенты k = m = n = 0,82. Из теоремы о треугольнике следов говорится, что высоты треугольника следов совпадают с аксонометрическими осями системы, соответствующей данному треугольнику. Следовательно, углы между аксонометрическими осями в прямоугольной изометрической проекции одинаковые и равны 120о рисунок 3, а. Так как треугольник следов в прямоугольной изометрии равносторонний и высоты его пересекаются между собой под углом в 120о, то кружности, лежащие в плоскостях, параллельных координатным плоскостям, П1, П2 и П3, проецируются в виде эллипсов одинакового соотношения больших и малых осей рисунок 3, б. Большая полуось таких эллипсов равна радиусу R изображаемой окружности, а малая – 0,58 R. В практике построения прямоугольных изометрических проекций допускается применять не дробные действительные коэффициенты искажения k = m = n = 0,8, а округленные до единицы или, как их принято называть, приведенные коэффициенты искажения k0 = m0 = n0 = 1.
Рисунок 3. Прямоугольная изометрическая проекция: а – расположение осей Наглядное изображение, построенное по приведенным коэффициентам, увеличивается в 1,22 раза (1:0,82 = 1,22) по сравнению с действительным изображением, соответствующим коэффициентам искажения 0,82. При таком увеличении большие полуоси эллипсов, показанных на рисунок 3, б, равны 1,22 R, а малые – 0,71 R. Прямоугольные изометрические проекции с действительными и приведенными коэффициентами искажения рекомендуются государственным стандартом (ГОСТ 2.317-69) для применения в техническом черчении.
|