Алгоритм и программа разложения степени числа по правилам арифметики вычетов
Алгоритм разложения степени числа
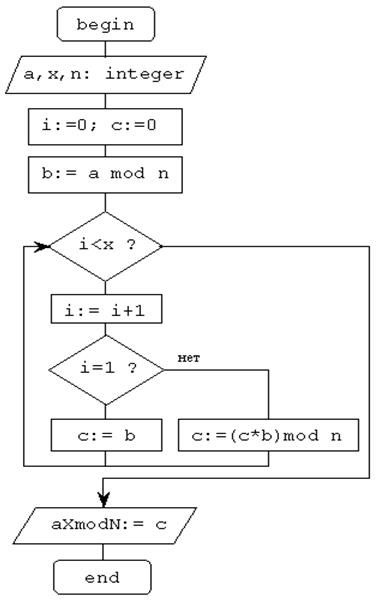
В Delphi имеется встроенная процедура возведения числа а в степень x y:=IntPower(a,x), содержащаяся в библиотеке Math. Недостаток данной процедуры, как ранее отмечено, состоит в переполнении формата результата процедуры y в оперативной памяти компьютера при относительно небольших значениях а и х. Разработаем собственную процедуру разложения степени числа по правилам арифметики вычетов, позволяющую исключить огромные результаты промежуточных вычислений. Для упорядочивания разложения выражения b= aХ mod n по степеням числа х результат вычисления будем записывать в переменную с, значения которой на каждой итерации разложения i определяется следующей логикой вычислений: i=1: b= a1 mod n → с = b ( i=2: b= a2 mod n = (a*a) mod n = ((a mod n) * (a mod n)) mod n =(b*b) mod n → c = (c*b) mod n ( i=3: b= a3 mod n = (a2*a) mod n = ((a2 mod n) * (a mod n)) mod n =(c*b) mod n → c = (c*b) mod n ( … i=x: ( В виде алгоритма представленная последовательность итераций приведена на рисунке 3.3. Согласно алгоритмы, исходный код функции разложения степени числа по правилам арифметики вычетов выгладит следующим образом: Function aXmodN(a,x,n: integer): integer; Var i,b,c: integer; Begin i:=0; b:= a mod n; c:=0; While i<x do Begin i:=i+1; If i=1 then c:=b else c:= (c*b) mod n; End; aXmodN:=c; end;{aXmodN}
Рисунок 3.3 – Алгоритм разложения степени числа
Таким образом, программный код вида y:=IntPower(a,x)mod n можно заменить выражением y:= aXmodN(a,x,n). Для исследования возможностей и преимуществ разработанной функции по сравнению с использованием встроенной процедурой Delphi y:=IntPower(a,x) напишем специальное приложение.
3.3.2.2 Приложение для исследования вариантов разложения степени числа
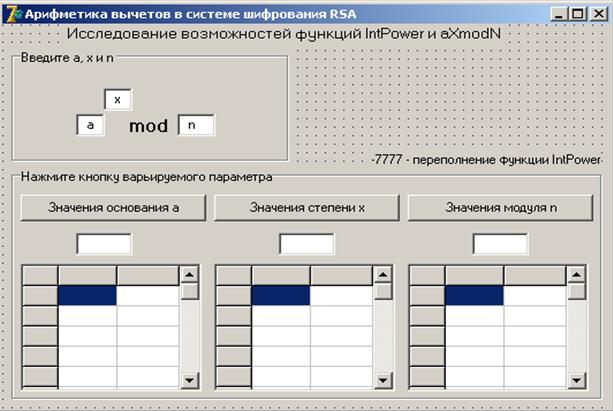
Рисунок 3.4 – Экранная форма приложения для исследования фунций y:=IntPower(a,x) и y:= aXmodN(a,x,n)
Рисунок 3.5 – Компоненты экранной формы приложения
|

 );
); );
); );
); ).
).