Модулярная арифметика (арифметика вычетов)
Общие понятия
Пусть а и п — натуральные числа. "Разделить число а на число п с остатком" — это значит найти целые числа q и r, удовлетворяющие условию
При этом число q называют неполным частным, а r - остатком от деления числа а на число п. Например. Число 51 разделить на 2: 51 = 25 . 2 + 1. Если остаток r равен нулю, то говорят, что число п делит число а, или, по-другому, п является делителем числа а. Целые числа а и b называют сравнимыми по модулю п, если их остатки при делении на п совпадают. Например, числа 51 и 27 сравнимы по модулю 2, так как остаток у обоих равен 1: 51 = 25 . 2 + 1, 27 = 13 . 2 + 1. Обычно для обозначения этого факта используется запись вида а ≡ b (mod п). Например, 51 ≡ 27 (mod 2). Отсюда, в частности, следует, что число п делит разность чисел а и b. Например: (51-27) / 2 = 24 /2 = 12. Для обозначения остатка часто используют бесскобочную запись вида b = a mod п. Например, запись вида 27 = 51 mod 2 обозначает остаток, равный единице. Операцию нахождения числа b=a modп называют приведением числа а по модулю п. Множество целых чисел Например, для b = 27, n = 2 - полная система вычетов числа 27 по модулю 2 составляет множество 3 ≡ 27 (mod 2) 5 ≡ 27 (mod 2) 7 ≡ 27 (mod 2) … 25 ≡ 27 (mod 2)
|
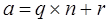, где 
.
, таких, что для любого целого числа b найдется 
со свойством 
, называется полной системой вычетов по модулю п. Обычно используется полная система вычетов {0, 1, …, n - 1}.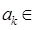
{ 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25}:
