Основная деталь. Між згинаючим моментом, поперечною силою і інтенсивністю розподіленого навантаження існують диференціальні залежності

 

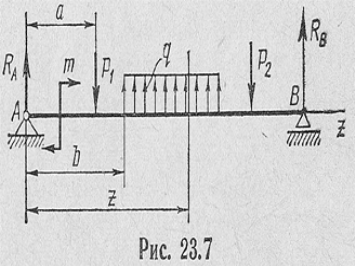
Між згинаючим моментом, поперечною силою і інтенсивністю розподіленого навантаження існують диференціальні залежності, в основі яких лежить теорема Журавського, названа так за ім'ям визначного російського інженера-мостобудівника Д. І.Журавського (1821 —1891). Цю теорему формулюють так: поперечна сила дорівнює першій похідній від згинаючого моменту по абсцисі пе-

рерізу балки Розглянемо балку, зображену на рис. 23.7. Початок координат

візьмемо на лівому кінці балки, а. вісь z напрямимо вправо (надалі ця обставина матиме важливе значення). На одній з ділянок балки проведемо переріз з поточною координатою z і запишемо рівняння згинаючого

моменту:

Мзг = Ra*z + m – P1(z-a)+ q(z-b)²/2.

 

Продиференціювавши цей вираз за координатою z, матимемо:

 

dMзг/dz = Ra- P1+q(z-b).

 

Вираз який стоїть у правій частині цієї рівності,— це поперечна сила

Q в перерізі z. Таким чином.

dMзг/dz = Q,

теорему доведено. Якщо рівняння згинаючих моментів {для ділянок з

рівномірно розподіленим навантаженням) продиференціювати вдруге, то

матимемо

d²M/dz² = dQ/dz = q

 

тобто друга похідна від згинаючого моменту або перша похідна від попереч-

ної сили за абсцисою перерізу балки дорівнює інтенсивності розподіленого

навантаження. Як відомо з вищої математики, за законом другої по-

хідної функції можна судити про опуклість або вгнутість кривої; відповід-

не правило слід використовувати для побудови епюр.

 

основная деталь

Всего 14 мотивов, из них: 8 - пятиугольных (№ 1,3,5,6,10,11,12,13) и 6 - шестиугольных (№ 2,4,7,8,9,14). Соединяем по фото...

Теперь нужно набить тушку синтепоном и сшить "попу", как на фото ниже... с одной стороны туловища сшить между собой грани шестиугольников № 7 и 8, соответственно с другой грани шестиугольников № 7 и 14, и точно так же грани № 8 и 9, соответственно с другой стороны грани многоугольников № 9 и 14...