Стратегии поиска.
Существуют две различные стратегии выбора точек, в которых производится вычисление значений функции. Если все точки задаются заранее, до начала вычислений, - это пассивная (параллельная) стратегия. Если эти точки выбираются последовательно в процессе поиска с учетом результатов предыдущих вычислений, - это последовательная стратегия. Примером реализации пассивной стратегии является метод равномерного поиска, примером последовательной стратегии является метод дихотомии. Стратегия поиска включает в себя три этапа: 1. выбор начального интервала неопределенности. Границы [a0, b0] интервала должны быть такими, чтобы функция f(x) была унимодальной. 2. Уменьшение интервала неопределенности. 3. Проверку условия окончания. Поиск заканчивается, когда длина текущего интервала неопределенности [aк, bк] оказывается меньше установленной величины. Ответом является множество точек, принадлежащих последнему интервалу неопределенности, среди которых каким-либо образом выбирается решение задачи x*. В некоторых методах заранее задается или находится количество N вычислений функции. В этом случае продолжительность поиска ограничена (пассивная стратегия). Для эвристического выбора начального интервала неопределенности применяется алгоритм Свенна. Алгоритм Свенна: 1) задать произвольно следующие параметры: x0 - некоторую точку, t > 0 - величину шага. Положить k=0; 2) вычислить значение функции в трех точках: x0 - t, x0, x0+ t; 3) проверить условие окончания: а) если
б) если в) если условие окончания не выполняется, то перейти к шагу 4; 4) определить величину: а) если б) если 5) найти следующую точку 6) проверить условие убывания функции: а) если f(xk+1) < f(xk) и если f(xk+1) < f(xk) и в обоих случаях положить k=k+1 и перейти к шагу 5; б) если При В результате имеем [a0, b0] - искомый начальный интервал неопределенности. Для оценки эффективности алгоритмов уменьшения интервала неопределенности при заданном числе N вычислений функции введем критерий. Определение 2. Характеристикой R(N) относительного уменьшения начального интервала неопределенности называется отношение длины интервала, получаемого в результате N вычислений функции, к длине начального интервала неопределенности:
Пример1. Найти начальный интервал неопределенности для поиска минимума функции f(x)=(x-5)2 Воспользуемся алгоритмом Свенна. 1. Зададим x0=1, t=1. Положим k=0. 20. Вычислим значения функции в точках x0- t =0, x0=1, x0 + t =2: f(0)=25, f(1)=16, f(2)=9. 30. 40. Так как f(0)>f(1)>f(2), то 50. Найдем следующую точку 60. f(x2)=(4-5)2=1, f(x1)= (2-5)2=9. Так как f(x2)=1 < f(x1) и Положим k=2 и перейдем к шагу 5. 51. Найдем следующую точку 61. Так как f(x3)=9 > f(x2)=1 и Поэтому начальный интервал неопределенности имеет вид [a0, b0]=[2, 8]. Метод равномерного поиска
|

 , то начальный интервал неопределенности найден:
, то начальный интервал неопределенности найден: ;
; , то функция не является унимодальной, а требуемый интервал неопределенности не может быть найден. Вычисления при этом прекращаются (рекомендуется задать другую начальную точку x0);
, то функция не является унимодальной, а требуемый интервал неопределенности не может быть найден. Вычисления при этом прекращаются (рекомендуется задать другую начальную точку x0); , то
, то  ; a0 = x0; x1 = x0 + t; k=1;
; a0 = x0; x1 = x0 + t; k=1; , то
, то  ; b0 = x0; x0 = x0 - t; k=1;
; b0 = x0; x0 = x0 - t; k=1; ;
;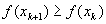 , то процедура завершается.
, то процедура завершается.
 - условия окончания не выполняются. Переходим к шагу 4.
- условия окончания не выполняются. Переходим к шагу 4. ; a0=1; x1=x0+ t =2; k=1
; a0=1; x1=x0+ t =2; k=1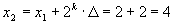 .
. , то a0=x1=2.
, то a0=x1=2.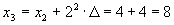 .
.


