Постановка задачи поиска безусловного минимума функции одной переменной. Стратегии поиска начального интервала неопределенности с помощью алгоритма Свенна.
1.Автоматизация электроподвижного состава / Ред. А.Н.Савоськин. М., Транспорт 1980, 310 с. 2.Якушев А.Я. Автоматическое управление электрическим подвижным составом, Учебное пособие, ч.1. С-Пб., ПГУПС, 1997, с.85. 3.Якушев А.Я. Автоматическое управление электрическим подвижным составом, Учебное пособие, ч.2. С-Пб., ПГУПС, 2001, с.86. Лабораторная работа №12
Тема: Приближенное вычисление экстремума функции в MathCAD (метод равномерного поиска). Цель: научиться вычислять безусловный минимум функции в MathCAD, используя алгоритм метода равномерного поиска. Порядок выполнения работы 1. Ознакомиться с теоретическими положениями. 2. Рассмотреть пример вычисления минимума функции в MathCAD. 3. Выполнить практическое задание. 4. Ответить на контрольные вопросы. Содержание отчета 1. Тема, цель работы. 2. Практическое задание: 2.1. Постановка задачи. 2.2. Результаты выполнения. 3. Ответы на контрольные вопросы. 4. Вывод. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Постановка задачи поиска безусловного минимума функции одной переменной. Стратегии поиска начального интервала неопределенности с помощью алгоритма Свенна. Постановка задачи Требуется найти безусловный минимум функции f(x) одной переменной, т.е. такую точку 1. Для методов одномерной минимизации типично задание информации о положении точки минимума с помощью начального интервала неопределенности L0=[a0,b0]. Предполагается, что точка минимума х* принадлежит интервалу L0, но ее точное значение неизвестно. 2. Большинство известных методов одномерной минимизации применяется для класса унимодальных функций. Определение 1. Функция f(x) называется унимодальной на интервале L0=[a0,b0], если она достигает глобального минимума на [a0,b0] в единственной точке x*, причем слева от x* эта функция строго убывает, а справа от x* строго возрастает. Если
Рис.1
|

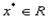 , что
, что 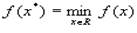 .
. , то f(x) > f(z), а если
, то f(x) > f(z), а если  , то f(y) < f(z) (рис.1).
, то f(y) < f(z) (рис.1).



