Примеры выполнения заданий, содержащих показательные уравнения
Пример 1. Укажите промежуток, которому принадлежит корень уравнения 1) (0; 1); 2)(1;2); 3) (2; 3); 4) (3; 4). Решение. Используя свойство степени (ах)у = аху, получаем:
Так как Поскольку 3,5 Ответ: 4.
Пример 2. Укажите промежуток, которому принадлежит корень уравнения 2 х-1 + 2 х+1 = 20. 1) (4; 5); 2) [3; 4]; 3) (2; 3); 4) [1; 2]. Решение. 2 х-1 + 2 х+1 = 20; х
Ответ: 2.
Пример 3. Найдите произведение корней уравнения
Решение.
Ответ: 1
Блок 3: Задания для самостоятельной работы 1) Тренажер. Определите методы решения уравнений и решите их:
2)Тренажёр. Решите уравнения: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. Тест Вариант 1.Указать промежуток, которому принадлежит корень уравнения ( 1. 2. Указать промежуток, которому принадлежит корень уравнения 3 1. 3. Указать промежуток, которому принадлежит корень уравнения 5 1. 4. Решите уравнение. В ответе укажите меньший корень 5. Решите уравнение 7x5 6. Решите уравнение 7. Решите уравнение 6 8. Указать промежуток, которому принадлежит корень уравнения 5 1. 9. Решите уравнение 3 10. Решите уравнение 3 Вариант 1. Указать промежуток, которому принадлежит корень уравнения 4 1. (-5;-2); 2.Указать промежуток, которому принадлежит корень уравнения 0,3 1. (-1;0); 3. Указать меньший корень уравнения 10 1. 5 2. 1 3. -1 4. 0. 4. Решить уравнение 5. Решить уравнение 3 6. Решить уравнение 7. Решить уравнение 8. Решите уравнение и выберите правильный ответ: 5 1. 1 2. ±2 3. нет решений 4. ±5 9. Решите уравнение 10. Решите уравнение 2x4
|

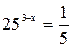

 = 5-1, то 52(З-х) = 5-1 Степени с одинаковым основанием равны, значит, равны их показатели: 2(3 - х) = -1; 6 - 2х = -1, - 2х = -7, х = 3,5
= 5-1, то 52(З-х) = 5-1 Степени с одинаковым основанием равны, значит, равны их показатели: 2(3 - х) = -1; 6 - 2х = -1, - 2х = -7, х = 3,5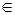 (3; 4), верным является ответ №4.
(3; 4), верным является ответ №4. + 2·2х = 20; 2х + 4∙2х = 40; 5 ·2х = 40; 2х = 8; х = 3;
+ 2·2х = 20; 2х + 4∙2х = 40; 5 ·2х = 40; 2х = 8; х = 3; = 243.
= 243. х1·х2 =
х1·х2 = 
 = -6
= -6
 ;
; .
.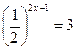 .
. .
. .
.
 .
.



 .
. .
. ,
, .
. .
. .
.





 .
.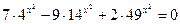 .
.
 )
)  =125.
=125. ;
;  ;
;  ;
;  .
. .
. ;
; 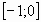 ;
; 
 ;
;  ;
;  .
. .
.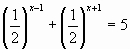
 .
. .
. ;
;  ;
; 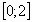 ;
;  .
.

 .
.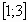 .
. .
.
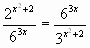
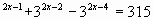

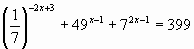

 -5=0.
-5=0.


