Примеры расчетов
Пример 24. Для рамы (рис.55,а) построить эпюру изгибающих моментов и выполнить все необходимые проверки расчета при условии, что жесткости всех элементов рамы одинаковы и равны EI.
Рис. 55 Определим число основных неизвестных – степень кинематической неопределимости рамы. Так как число неизвестных угловых перемещений равно числу жестких узлов рамы, то ny=2. Число независимых линейных смещений nл=1. Действительно, узлы рамы 4 и 5 не могут перемещаться по вертикали из-за опорных закреплений 1 и 2 и принятой гипотезы о нерастяжимости стержней и неизменности их длинны при изгибе. Для них возможно только горизонтальное перемещение, которое будет одинаковым для узлов 4, 5 и 3 вследствие того, что они связаны между собой стержнями 4-5 и 5-3. Таким образом, степень кинематической неопределимости рамы:
Образуем основную систему, введя связи, препятствующие угловым и линейному смещениям, и обозначим предполагаемые направления (произвольно) трех неизвестных перемещений (рис.55,б). Используя приведенную выше вспомогательную таблицу метода перемещений, построим эпюры изгибающих моментов
При построении всех указанных эпюр нужно четко представлять себе перемещение оси каждого стержня, вызванное заданным единичным смещением; это позволит установить положение сжатых волокон элементов рамы и правильно изобразить эпюры моментов. Система канонических уравнений имеет вид:
Для определения коэффициентов и свободных членов этих уравнений, которые представляют собой реактивные усилия в наложенных связях, применим статический способ. Для этого вырежем сначала узел 4 и рассмотрим условия его равновесия в случаях, представленных на рис.55,в-е, т.е. определим коэффициенты первой строки канонических уравнений. На рис.56,а-г показан узел 4 с действующими на него моментами со стороны отброшенных частей рамы и реактивными моментами в защемлении (первой связи). Из условий равновесия этого узла получим:
Отрицательный знак в двух последних случаях объясняется тем, что направления реактивных моментов Аналогично определим коэффициенты второго канонического уравнения. Для этого вырежем из рамы узел 5 и рассмотрим условия его равновесия при тех же четырех воздействиях на основную систему (рис.55,в-е).
Рис. 56
Из рис.56,д-з следует:
Для определения коэффициентов третьего уравнения, представляющих собой реакции во введенном стержне (третьей связи), рассечем стойки рамы и рассмотрим условия равновесия ее средней части, содержащей введенный стержень (рис.57,а-г). При этом под условием равновесия будем понимать равенство нулю суммы проекций всех сил, приложенных к выделенной части рамы, на горизонтальную ось:
Рис. 57
Из рис.57,а-г следует:
Проверку вычисленных коэффициентов и свободных членов можно осуществить способом перемножения эпюр. Для выполнения универсальной проверки построим суммарную единичную эпюру изгибающих моментов
Сумма коэффициентов при неизвестных составляет:
коэффициенты вычислены правильно. Для проверки свободных членов канонических уравнений необходимо построить эпюру изгибающих моментов
Два возможных варианта эпюры
Подставляя найденные значения коэффициентов и свободных членов в исходную систему канонических уравнений, получим:
Решение системы (4.17) дает следующие значения неизвестных:
Единичные эпюры моментов (рис.55,в-д) теперь можно "исправить", т.е. умножить на соответствующие значения неизвестных. При этом вторая эпюра
Рис. 58 Выполним статическую проверку. Для этого вырежем узлы 4 и 5, а также среднюю часть рамы (рис.59,а-в) и убедимся в выполнении условий равновесия. Как уже говорилось, статическая проверка является достаточным критерием правильности выполненного расчета. Тем не менее, выполним дополнительно кинематическую проверку. Для этого построим суммарную единичную эпюру В заключение отметим, что степень статической неопределимости рассмотренной рамы равна пяти, а это означает, что трудоемкость расчета данной системы методом сил значительно выше, чем при использовании метода перемещений.
Рис. 59 Пример 25. Для рамы с наклонными стойками (рис.60,а) построить эпюры M, Q, N при условии, что жесткость ригеля (2-3) в два раза больше чем жесткость наклонных стоек 1-2 и 3-4. Определяем степень кинематической неопределимости рамы:
Основную систему образуем путем введения защемления в узле 2 и горизонтального опорного стержня в узле 3 (рис.60,б). Для определения неизвестных перемещений z1 и z2 по направлениям введенных связей запишем систему канонических уравнений метода перемещений:
Используя вспомогательную таблицу метода перемещений, построим эпюры изгибающих моментов от единичного угла поворота Отметим, что узловая нагрузка
Рис. 60 Для определения указанных перемещений построим для шарнирной схемы, образованной из заданной рамы (рис.61,а),полярный план перемещений (рис.61,б). Из этого плана определим взаимное перемещение концов стержней:
Так как введенное защемление препятствует повороту узла 2, то от найденных взаимных смещений произойдет изгиб стержней (рис.61,в). Эпюра моментов
Рис. 61
Коэффициенты r11, r12 и свободный член R1F определим из условия равновесия узла 2:
Для определения коэффициента
откуда
откуда Условия равновесия узла 3 (рис.62,б) позволяют получить:
Аналогично можно определить и свободный член
Рис. 62 Использование статического способа для вычисления коэффициентов
Для определения свободного члена
После подстановки вычисленных коэффициентов в уравнения (4.19) получим:
откуда:
Окончательную эпюру моментов (рис.63,б) строим по формуле:
Соответствующие ей эпюры поперечных и продольных сил показаны на рис.63,в,г.
Рис. 63 Читателю предлагается самостоятельно убедиться в том, что для окончательных эпюр выполняются статические проверки: в узле 2 изгибающие моменты уравновешены; а силы, действующие на верхнюю отсеченную часть рамы, удовлетворяют условиям равновесия Пример 26. Используя упрощения, связанные с симметрией заданной рамы (рис.64,а), построить эпюру изгибающих моментов, при условии, что жесткости всех стержней одинаковы и равны EI. Степень кинематической неопределимости рамы:
При выборе основной системы метода перемещений (рис.64,б) используем условия симметрии. Сгруппируем неизвестные углы поворота, т.е. угол поворота узла 2 представим в виде суммы двух углов поворота Горизонтальное перемещение ригеля Для определения групповых неизвестных
Как видно, форма канонических уравнений при группировке неизвестных остается прежней. Но здесь все эпюры от единичных неизвестных (рис. 64, в-д) будут только симметричными или обратносимметричными, а канонические уравнения распадутся на две независимые системы, содержащие только симметричные или только обратносимметричные групповые неизвестные. При этом неизвестные перемещения узлов, расположенных на оси симметрии, всегда обладают симметрией или обратной симметрией и поэтому не группируются.
Рис. 64 Значения единичных коэффициентов и свободных членов в уравнениях (4.20) приобретают несколько иной смысл, чем ранее. Здесь При использовании статического способа для коэффициентов и свободных членов канонических уравнений (4.20) получим:
где индексами "л" и "n" обозначены соответственно левая (узел 2) и правая (узел Вследствие равенства нулю четырех коэффициентов система канонических уравнений (4.20) распадается на две системы, а точнее – на систему уравнений относительно неизвестных Z1 и Z3 и уравнение относительно Z2:
В результате решения получим следующее значения неизвестных:
В этом примере обозначено:
Окончательная эпюра моментов (рис.65) имеет вид:
Рис. 65 Литература: 1. Дарков А.В., Шапашников Н.Н. Строительная механика: Учеб. для строит. спец. вузов. – 8-е изд., перераб. и доп. – М.: Высш. шк., 1986. – 607с.: ил. 2.Руководство к практическим занятиям по курсу строительной механики (статика стержневых систем): Учеб. особие для студентов вузов /Г.К. Клейн, Н.Н. Леонтьев, М. Г. Ванюшенков и др.; Под ред. Г.Г. Клейна. 4-е изд., перераб. и доп. – М.: Высшая школа /1980. – 384с.: ил. 3.Справочник по сопротивлению материалов /Писаренко Г.С., Яковлев А.П., Матвеев В.В.; Отв. ред. Писаренко Г.С. – 2-е изд., перераб. и доп. – Киев: Наук. думка, 1988. – 736с.: ил. 4.Строительная механика: Учебник для вузов /Ю.И. Бутейко, Н.А. Засядько, С.Н. Кан и др.; Под ред. Ю.И. Бутенко. – К.: Выща шк., 1989. – 479с.; ил. 5.Строительная механика. Стержневые системы: Учебник для вузов /А.Ф. Смирнов, А.В. Александров, Б.Я. Лащенков, Н.Н. Шапошников; Под ред. А.Ф. Смирнова. – М.: Стройиздат, 1981. – 512с; ил. Содержание Введение....................................................................................................... 3 Глава 1...................................................................................................... 4 Построение эпюр внутренних силовых факторов................................ 4 1.1 Внутренние силы упругости. Метод сечений............................. 4 1.2 Виды сопротивлений...................................................................... 6 1.3 Виды опорных закреплений......................................................... 7 1.4 Построение эпюр продольных сил.............................................. 8 1.4 Построение эпюр крутящих моментов........................................ 9 ............................................................................................................. 10 1.6 Правила контроля эпюр и.......................................................... 10 1.7 Построение эпюр поперечных сил и изгибающих моментов в балках.................................................................................................................... 11 1.8 Консольные балки........................................................................ 12 1.9 Дифференциальные зависимости между.................................... 14 1.10 Балки на двух опорах................................................................ 15 1.11 Правила контроля эпюр Qу и Mx............................................. 19 1.12 Другие подходы к построению эпюр внутренних силовых факторов.................................................................................................................... 20 1.13 Построение эпюр для плоских рам........................................... 21 1.14 Рамы с жесткой заделкой........................................................... 23 1.15 Рамы на двух шарнирных опорах............................................ 28 1.16 Рамы на двух опорах с промежуточным шарниром............... 34 1.17 Построение эпюр в плоско-пространственных системах......... 37 1.18 Построение эпюр в ломаных стержнях..................................... 44 Глава 2 Определение перемещений в упругих системах........................ 51 2.1 Обобщенные силы и обобщенные перемещения........................ 52 2.2 Работа внешних сил. Потенциальная энергия............................ 53 2.3 Теорема о взаимности работ....................................................... 57 2.4 Теорема о взаимности перемещений........................................... 59 2.5 Вычислений перемещений методом Мора.................................. 60 Примеры расчетов............................................................................. 63 2.7 Правило Верещагина................................................................... 67 2.8 Основные варианты перемножения эпюр.................................. 69 Глава 3...................................................................................................... 77 Построение эпюр в статически неопределимых истемах. Метод сил.... 77 3.1 Особенности статически неопределимых систем и методы их расчета.................................................................................................................... 77 3.2 Канонические уравнения метода сил.......................................... 79 3.3 Алгоритм расчета методом сил................................................... 81 3.4 Выбор основной системы........................................................... 82 3.5 Вычисление коэффициентов и свободных членов канонических уравнений................................................................................................... 84 3.6 Универсальная проверка коэффициентов и свободных членов канонических уравнений........................................................................... 85 3.7 Построение окончательных эпюр внутренних силовых факторов 87 3.8 Проверка окончательной эпюры изгибающих моментов......... 88 3.9 Определение перемещений в статически неопределимых системах 89 3.10 Расчет симметричных систем методом сил.............................. 90 3.10 Примеры расчетов.................................................................... 92 Глава 4..................................................................................................... 119 Построение эпюр в статически неопределимых системах. Метод перемещений.......................................................................................................................... 119 4.1 Сущность метода........................................................................ 119 4.2 Вспомогательная таблица метода перемещений..................... 123 4.3 Каноническое уравнение метода перемещений....................... 130 4.4 Алгоритм расчета систем методом перемещений.................... 133 4.5 Методы вычисления коэффициентов и свободных членов канонических уравнений................................................................................................. 133 4.6 Проверки метода перемещений............................................... 134 4.7 Использование симметрии при расчете рам методом перемещений 137 4.8 Примеры расчетов.................................................................... 138 Литература:.......................................................................................... 155 Содержание.......................................................................................... 156
|



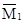 ,
,  ,
,  от единичных перемещений введенных связей по заданным направлениям и эпюру
от единичных перемещений введенных связей по заданным направлениям и эпюру  от действия нагрузки на основную систему (рис.55,в-е). Для удобства на этих рисунках использованы следующие обозначения:
от действия нагрузки на основную систему (рис.55,в-е). Для удобства на этих рисунках использованы следующие обозначения:




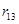 и
и  противоположны заданному направлению угла поворота Z1 первой связи.
противоположны заданному направлению угла поворота Z1 первой связи.

 Отличные от нуля проекции дадут искомые реакции во введенном стержне и поперечные силы, приложенные в местах рассечения стоек и определяемые по эпюрам
Отличные от нуля проекции дадут искомые реакции во введенном стержне и поперечные силы, приложенные в местах рассечения стоек и определяемые по эпюрам  ,
,  ,
,  , MF.
, MF.

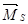 , представляющую собой сумму единичных эпюр
, представляющую собой сумму единичных эпюр 
 т.е.
т.е. от внешней нагрузки, приложенной в любой статически определимой системе, образованной из заданной рамы, и перемножить ее с эпюрой
от внешней нагрузки, приложенной в любой статически определимой системе, образованной из заданной рамы, и перемножить ее с эпюрой 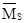 :
:

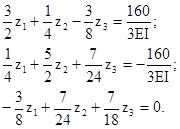 (4.17)
(4.17)
 (4.18)
(4.18)


 (4.19)
(4.19) и от внешней нагрузки (рис.60,в,г).
и от внешней нагрузки (рис.60,в,г). не вызывает изгибающих моментов в основной системе. Для построения эпюры моментов от единичного горизонтального перемещения
не вызывает изгибающих моментов в основной системе. Для построения эпюры моментов от единичного горизонтального перемещения  второй связи необходимо знать, как перемещаются в этом случае концы стержней рамы. Перемещение узла 3 происходит по направлению, перпендикулярному линии 3-4 (искомое перемещение
второй связи необходимо знать, как перемещаются в этом случае концы стержней рамы. Перемещение узла 3 происходит по направлению, перпендикулярному линии 3-4 (искомое перемещение  является горизонтальной проекцией полного смещения узла 3, а узла 2 – по направлению, перпендикулярному линии 1-2. В результате этого происходит относительное перемещение узлов 2 и 3 по вертикали.
является горизонтальной проекцией полного смещения узла 3, а узла 2 – по направлению, перпендикулярному линии 1-2. В результате этого происходит относительное перемещение узлов 2 и 3 по вертикали.

 может быть теперь построена с помощью вспомогательной таблицы метода перемещений (рис.61,г).
может быть теперь построена с помощью вспомогательной таблицы метода перемещений (рис.61,г).

 , представляющего собой реакцию во введенном стержне от единичного смещения
, представляющего собой реакцию во введенном стержне от единичного смещения  , рассмотрим условия равновесия ригеля, отсеченного от стоек. Для этого необходимо определить поперечные и продольные силы, соответствующие эпюре
, рассмотрим условия равновесия ригеля, отсеченного от стоек. Для этого необходимо определить поперечные и продольные силы, соответствующие эпюре 






 по эпюре
по эпюре 







 и
и 

 и
и  , а поворот узла
, а поворот узла  , симметричного узлу 2, - в виде разности углов
, симметричного узлу 2, - в виде разности углов  является обратносимметричным неизвестным, так как узел
является обратносимметричным неизвестным, так как узел 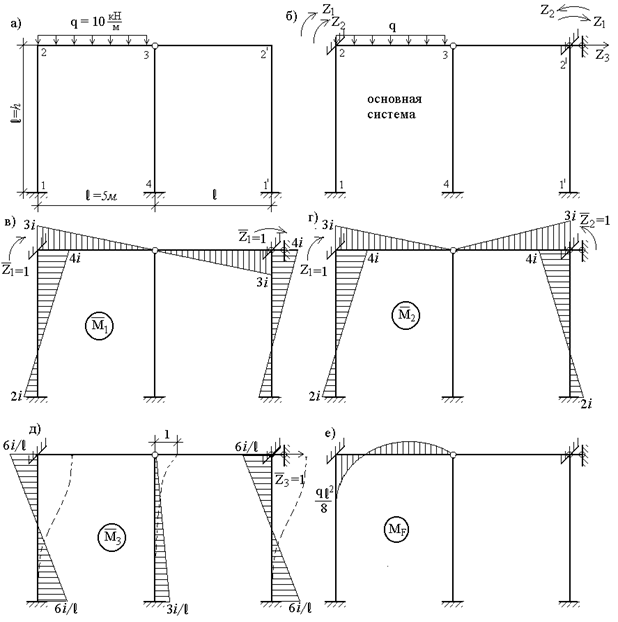
 и
и  - обобщенные реакции, соответствующие обобщенному перемещению
- обобщенные реакции, соответствующие обобщенному перемещению  от парного смещения
от парного смещения  и от внешней нагрузки. Эти обобщенные реакции определяются как алгебраические суммы простых реакций в связях, которые одновременно смещаются при групповом парном перемещении
и от внешней нагрузки. Эти обобщенные реакции определяются как алгебраические суммы простых реакций в связях, которые одновременно смещаются при групповом парном перемещении  . Положительные направления простых реакций принимаются, как и ранее, совпадающими с задаваемыми направлениями перемещений тех связей, в которых они определяются.
. Положительные направления простых реакций принимаются, как и ранее, совпадающими с задаваемыми направлениями перемещений тех связей, в которых они определяются.






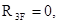
 и
и  ) определены из условия равновесия
) определены из условия равновесия  отсеченного ригеля рамы.
отсеченного ригеля рамы.







