Теоретические упражнения. Троцкист Христиан Георгиевич Раковский (бывший полпред СССР в Англии и Франции), на допросе в НКВД (протокол от 26.01.1938 г.) утверждал
Теоретические упражнения 1. Пусть 2. Написать уравнение линии, на которой могут находиться точки перегиба графиков решений уравнения 3. Написать уравнение линии, на которой могут находиться точки графиков решений уравнения 4. Линейное дифференциальное уравнение останется линейным при замене независимой переменной 5. Доказать, что линейное дифференциальное уравнение остается линейный при преобразовании искомой функции
Здесь 6. Составить общее.решение уравнения 7. Показать, что произвольные дважды дифференцируемые функции
8. Составить однородное линейное дифференциальное уравнение второго порядка, имеющее решения Показать, что функции Убедиться в том, что определитель Вронского для этих функций равен нулю в точке 9. Найти общее решение неоднородного линейного дифференциального уравнения второго порядка, если известны три линейно-независимые частные его решения 10. Доказать, что для того чтобы любое решение линейного однородного дифференциального уравнения с постоянными коэффициентами удовлетворяло условию
|

 — решение дифференциального уравнения
— решение дифференциального уравнения 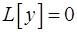 . Показать, что введение новой искомой функции
. Показать, что введение новой искомой функции  приводит к дифференциальному уравнению, допускающему понижение порядка.
приводит к дифференциальному уравнению, допускающему понижение порядка. .
. , где функция
, где функция  произвольная, но дифференцируемая достаточное число раз: Доказать это утверждение для линейного дифференциального уравнения второго порядка.
произвольная, но дифференцируемая достаточное число раз: Доказать это утверждение для линейного дифференциального уравнения второго порядка. .
. — новая искомая функция,
— новая искомая функция,  и
и  — произвольные, но достаточное число раз дифференцируемые функции.
— произвольные, но достаточное число раз дифференцируемые функции. , если известно ненулевое частное решение
, если известно ненулевое частное решение  и
и  являются решениями линейного дифференциального уравнения.
являются решениями линейного дифференциального уравнения.
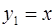 ,
,  .
. и
и  линейно -независимы в интервале
линейно -независимы в интервале 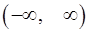 .
. . Почему это не противоречит необходимому условию линейной независимости системы решений линейного однородного дифференциального уравнения?
. Почему это не противоречит необходимому условию линейной независимости системы решений линейного однородного дифференциального уравнения? и
и  .
. , необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные действительные части.
, необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные действительные части.


