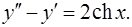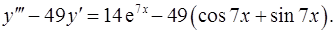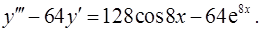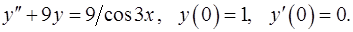Расчетные задания
Задача 1. Найти общий интеграл дифференциального уравнения. (Ответ представить в виде 1.1. 1.3. 1.5. 1.7. 1.9. 1.11. 1.13. 1.15. 1.17. 1.19. 1.21. 1.23. 1.25. 1.27. 1.29. 1.31.
Задача 2. Найти общий интеграл дифференциального уравнения. 2.1. 2.3. 2.5. 2.7. 2.9. 2.11. 2.13. 2.15. 2.17. 2.19. 2.21. 2.23. 2.25. 2.27. 2.29. 2.31.
Задача 3. Найти общий интеграл дифференциального уравнения. 3.1. 3.3. 3.5. 3.7. 3.9. 3.11. 3.13. 3.15. 3.17. 3.19. 3.21. 3.23. 3.25. 3.27. 3.29. 3.31.
Задача 4. Найти решение задачи Коши. 4.1. 4.3. 4.5. 4.7. 4.9. 4.11. 4.13. 4.15. 4.17. 4.19. 4.21. 4.23. 4.25. 4.27. 4.29. 4.31.
Задача 5. Решить задачу Коши. 5.1. 5.2. 5.3. 5.4. 5.5. 5.6. 5.7. 5.8. 5.9. 5.10. 5.11. 5.12. 5.13. 5.14. 5.15. 5.16. 5.17. 5.18. 5.19. 5.20. 5.21. 5.22. 5.23. 5.24. 5.25. 5.26. 5.27. 5.28. 5.29. 5.30. 5.31. Задача 6. Найти решение задачи Коши. 6.1. 6.2. 6.3. 6.4. 6.5. 6.6. 6.7. 6.8. 6.9. 6.10. 6.11. 6.12. 6.13. 6.14. 6.15. 6.16. 6.17. 6.18. 6.19. 6.20. 6.21. 6.22. 6.23. 6.24. 6.25. 6.26. 6.27. 6.28. 6.29. 6.30. 6.31.
Задача 7. Найти общий интеграл дифференциального уравнения. 7.1. 7.2. 7.3. 7.4. 7.5. 7.6. 7.7. 7.8. 7.9. 7.10. 7.11. 7.12. 7.13. 7.15. 7.17. 7.18. 7.20. 7.21. 7.22. 7.23. 7.24. 7.25. 7.26. 7.27. 7.28. 7.29. 7.30. 7.31. Задача 8. Для данного дифференциального уравнения методом изоклин построить интегральную кривую, проходящую через точку 8.1. 8.3. 8.5. 8.7. 8.9. 8.11. 8.13. 8.15. 8.17. 8.19. 8.21. 8.23. 8.25. 8.27. 8.29. 8.31. Задача 9. Найти линию, проходящую через точку 9.1. 9.3. 9.5. Найти линию, проходящую через точку 9.6. 9.8. 9.10. Найти линию, проходящую через точку 9.11. 9.13. 9.15. Найти линию, проходящую через точку 9.16. 9.18. 9.20. Найти линию, проходящую через точку 9.21. 9.23. 9.25. Найти линию, проходящую через точку 9.26. 9.28. 9.30.
Задача 10. Найти общее решение дифференциального уравнения. 10.1. 10.3. 10.5. 10.7. 10.9. 10.11. 10.13. 10.15. 10.17. 10.19. 10.21. 10.23. 10.25. 10.27. 10.29. 10.31.
Задача 11. Найти решение задачи Коши. 11.1. 11.2. 11.3. 11.4. 11.5. 11.6. 11.7. 11.8. 11.9. 11.10. 11.11. 11.12. 11.13. 11.14. 11.15. 11.16. 11.17. 11.18. 11.19. 11.20. 11.21. 11.22. 11.23. 11.24. 11.25. 11.26. 11.27. 11.28. 11.29. 11.30. 11.31.
Задача 12. Найти общее решение дифференциального уравнения. 12.1. 12.3. 12.5. 12.7. 12.9. 12.11. 12.13. 12.15. 12.17. 12.19. 12.21. 12.23. 12.25. 12.27. 12.29. 12.31.
Задача 13. Найти общее решение дифференциального уравнения. 13.1. 13.2. 13.3. 13.4. 13.5. 13.6. 13.7. 13.8. 13.9. 13.10. 13.11. 13.12. 13.13. 13.14. 13.15. 13.16. 13.17. 13.18. 13.19. 13.20. 13.21. 13.22. 13.23. 13.24. 13.25. 13.26. 13.27. 13.28. 13.29. 13.30. 13.31.
Задача 14. Найти общее решение дифференциального уравнения. 14.1. 14.3. 14.5. 14.7. 14.9. 14.11. 14.13. 14.15. 14.17. 14.19. 14.21. 14.23. 14.25. 14.27. 14.29. 14.31.
Задача 15. Найти общее решение дифференциального уравнения. 15.1. 15.2. 15.3. 15.4. 15.5. 15.6. 15.7. 15.8. 15.9. 15.10. 15.11. 15.12. 15.13. 15.14. 15.15. 15.16. 15.17. 15.18. 15.19. 15.20. 15.21. 15.22. 15.23. 15.24. 15.25. 15.26. 15.27. 15.28. 15.29. 15.30. 15.31.
Задача 16. Найти решение задачи Коши. 16.1. 16.2. 16.3. 16.4. 16.5. 16.6. 16.7. 16.8. 16.9. 16.10. 16.11. 16.12. 16.13. 16.14. 16.15. 16.16. 16.17. 16.18. 16.19. 16.20. 16.21. 16.22. 16.23. 16.24. 16.25. 16.26. 16.27. 16.28. 16.29. 16.30. 16.31.
|

 .)
.) 1.2.
1.2. 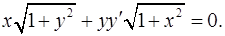
 1.4.
1.4. 
 1.6.
1.6. 
 1.8.
1.8. 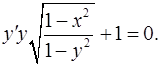
 1.10.
1.10. 
 1.12.
1.12. 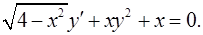
 1.14.
1.14. 
 1.16.
1.16. 
 1.18.
1.18. 
 1.20.
1.20. 
 1.22.
1.22. 
 1.24.
1.24. 
 1.26.
1.26. 

 1.28.
1.28. 
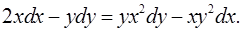 1.30.
1.30. 
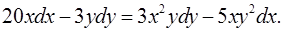
 2.2.
2.2. 
 2.4.
2.4. 
 2.6.
2.6. 
 2.8.
2.8. 
 2.10.
2.10. 
 2.12.
2.12. 
 2.14.
2.14. 
 2.16.
2.16. 
 2.18.
2.18. 
 2.20.
2.20. 
 2.22.
2.22. 
 2.24.
2.24. 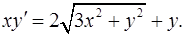
 2.26.
2.26. 
 2.28.
2.28. 
 2.30.
2.30. 

 3.2.
3.2. 
 3.4.
3.4. 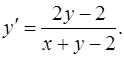
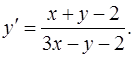 3.6.
3.6. 
 3.8.
3.8. 
 3.10.
3.10. 
 3.12.
3.12. 
 3.14.
3.14. 
 3.16.
3.16. 
 3.18.
3.18. 
 3.20.
3.20. 
 3.22.
3.22. 
 3.24.
3.24. 
 3.26.
3.26. 
 3.28.
3.28. 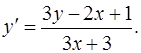
 3.30.
3.30. 

 4.2.
4.2. 
 4.4.
4.4. 
 4.6.
4.6. 
 4.8.
4.8. 
 4.10.
4.10. 
 4.12.
4.12. 
 4.14.
4.14. 
 4.16.
4.16. 
 4.18.
4.18. 
 4.20.
4.20. 
 4.22.
4.22. 
 4.24.
4.24. 
 4.26.
4.26. 
 4.28.
4.28. 
 4.30.
4.30. 










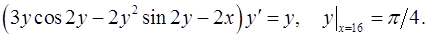





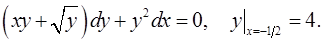








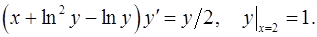





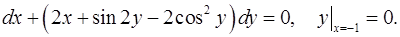





























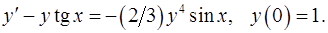













 7.14.
7.14. 
 7.16.
7.16. 

 7.19.
7.19. 












 .
. 8.2.
8.2. 
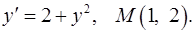 8.4.
8.4. 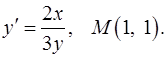
 8.6.
8.6. 
 8.8.
8.8. 
 8.10.
8.10. 
 8.12.
8.12. 
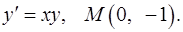 8.14.
8.14. 
 8.16.
8.16. 
 8.18.
8.18. 
 8.20.
8.20. 
 8.22.
8.22. 
 8.24.
8.24. 
 8.26.
8.26. 
 8.28.
8.28. 
 8.30.
8.30. 

 и обладающую тем свойством, что в любой ее точке
и обладающую тем свойством, что в любой ее точке  с концом на оси
с концом на оси  имеет длину, равную
имеет длину, равную  , и образует острый угол с положительным направлением оси
, и образует острый угол с положительным направлением оси  9.2.
9.2. 
 9.4.
9.4. 

 (считая от оси
(считая от оси  9.7.
9.7. 
 9.9.
9.9. 

 9.12.
9.12. 
 9.14.
9.14. 

 9.17.
9.17.  9.19.
9.19. 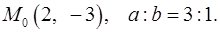

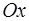 имеет проекцию на ось
имеет проекцию на ось  9.22.
9.22. 
 9.24.
9.24. 

 9.27.
9.27. 
 9.29.
9.29. 
 9.31.
9.31. 
 10.2.
10.2. 
 10.4.
10.4. 
 10.6.
10.6. 
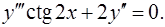 10.8.
10.8. 
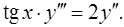 10.10.
10.10. 
 10.12.
10.12. 
 10.14.
10.14. 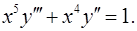
 10.16.
10.16. 
 10.18.
10.18. 
 10.20.
10.20. 
 10.22.
10.22. 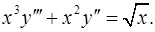
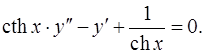 10.24.
10.24. 
 10.26.
10.26. 
 10.28.
10.28. 
 10.30.
10.30. 























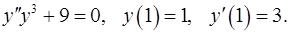




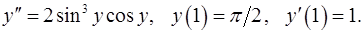



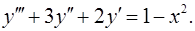 12.2.
12.2. 
 12.4.
12.4. 
 12.6.
12.6. 
 12.8.
12.8. 
 12.10.
12.10. 
 12.12.
12.12. 
 12.14.
12.14. 
 12.16.
12.16. 
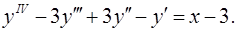 12.18.
12.18. 
 12.20.
12.20. 
 12.22.
12.22. 
 12.24.
12.24. 
 12.26.
12.26. 
 12.28.
12.28. 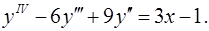
 12.30.
12.30. 










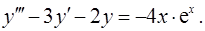












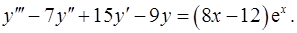

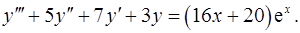






 14.2.
14.2. 
 14.4.
14.4. 
 14.6.
14.6. 
 14.8.
14.8. 
 14.10.
14.10. 
 14.12.
14.12. 
 14.14.
14.14. 
 14.16.
14.16. 
 14.18.
14.18. 
 14.20.
14.20. 
 14.22.
14.22. 
 14.24.
14.24. 
 14.26.
14.26. 
 14.28.
14.28. 
 14.30.
14.30.