В стационарном режиме температура тела постоянна во времени ( ). В этом случае
Это выражение называется уравнением Пуассона. Если теплоемкость вещества мала (с®0), то уравнением Пуассона можно пользоваться и в случае переменной во времени температуры (квазистационарное поле). 3. При отсутствии внутри тела источников тепла в стационарном режиме (qИ = 0;
Во многих практических задачах температурное поле тела можно считать с той или иной степенью приближения одномерным. Если форма изотермических поверхностей близка к плоскости, то, выбрав направление оси ОХ вдоль нормали к этим поверхностям, будем иметь
И уравнение Лапласа
Если изотермические поверхности представляют собой коаксиальные цилиндры, температура является функцией только одной координаты r – расстояния от оси цилиндра, и, переходя от декартовой системы координат к цилиндрической, оператор Лапласа можно записать
Если изотермические поверхности являются концентрическими сферами, то температура зависит также от одной координаты r – расстояния от центра сферы, и, переходя к сферической системе координат, оператор Лапласа принимает вид
|
(3.22)
),
Т = 0 – уравнение Лапласа. (3.23)
,
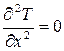. (3.24)
(3.25)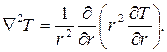
(3.26)
