III.2. Местные сопротивления и расчет трубопроводов
Потери энергии потока на поддержание движения в таких областях называются местными потерями напора hм. Они сконцентрированы на небольших (в сравнении с длиной трубы) участках. Местные потери определяются по формуле Вейсбаха:
где ζм – безразмерный коэффициент местного сопротивления. Величины ζм для различных видов местных сопротивлений определяют экспериментально. Сведения по коэффициентам местных сопротивлений содержатся в гидравлических справочниках и таблицах (например, в [Л.4]). В том случае, когда поток, проходя: через местные сопротивления, меняет сечение, ζм обычно определяют для скоростного напора в трубе после сопротивления. В частности, для резкого расширения (рис. 12, а)
где
Для резкого сжатия потока (рис. 12, б)
где Гидравлический расчет трубопроводов. При расчете трубопроводов обычно решаются следующие характерные задачи: 1. Определение напора H, необходимого для обеспечения заданного расхода Q в трубопроводе. 2. Определение расхода Q в заданном трубопроводе при известном напоре H. 3. Определение диаметров труб, обеспечивающих заданный расход при известном напоре. Трубопроводы делят на гидравлически длинные, в которых местные потери напора пренебрежимо малы по сравнению с потерями на длине, и гидравлически короткие, в которых эти виды потерь сравнимы по величине. Потери напора в последовательно размещенных на трубопроводе местных сопротивлениях и сопротивлениях по длине труб суммируются. Поэтому весь располагаемый напор равен сумме потерь (в случае истечения в атмосферу к нему добавляется еще скоростной напор вытекающей струи). При решении задачи 1 (определение напора при заданном расходе) вычисляются скорости в трубах. По формуле Вейсбаха (III.6) определяются местные потери. Вычисляются числа Рейнольдса, по Re и относительной шероховатости труб определяются области сопротивления, для которых находят гидравлические коэффициенты трения λтр. По формуле Дарси находят потери по длине и определяют полный напор:
Решение задачи 2 (определение расхода при заданном напоре) осложняется неопределенностью выбора λтр. Если при квадратичном сопротивлении λтр не зависит от скорости, то в остальных областях сопротивления λтр = f(Re), т. е. зависит от искомой скорости течения. Поэтому приходится решать задачу способом последовательного приближения. Может использоваться, в частности, такой графоаналитический метод. Задаваясь различными величинами скорости, определяют соответствующие величины расхода (по сути дела решая задачу 1) и строят график зависимости Н = f(Q). По исходной величине H определяют из этого графика соответствующий, расход Q. Пример. Рассмотрим истечение из бака через трубопровод, показанный на рис. 13. Пусть задан напор Н, требуется определить расход Q и построить пьезометрическую и гидродинамическую линию.
Составляя уравнение Бернулли для сечений 0–0 и 2–2, имеем
где
Подставляя это значение hu в уравнение (III.7а) и выражая скорость u1 через u2 из уравнения неразрывности (II.5а), т.е.
или
где коэффициент сопротивления системы ζс есть сумма коэффициентов сопротивления местных и по длине, приведенных к скорости в выходном сечении. Если диаметр труб и напор Н достаточно велики, можно полагать, что область сопротивления – квадратичная; определив гидравлические коэффициенты трения λтр1 и λтр2 по относительной шероховатости труб, вычисляем ζс и из формулы (III.7) – скорость течения. Правомерность сделанного выбора λтр проверяем, сопоставляя получившиеся числа Рейнольдса с зависимостями табл. 3. Если вычисленные скорости не обеспечивают достаточной величины чисел Рейнольдса для достижения квадратичного сопротивления, применяем графоаналитический метод решения. Задаваясь несколькими значениями скорости Полученные скорости в трубах позволяют определить потери напора в различных участках трубопровода, т. е. слагаемые правой части уравнения (III.7б). Откладывая последовательно эти потери на диаграмме уравнения Бернулли (рис. 13), получаем гидродинамическую линию Е–Е. Пьезометрическая линия, показанная на рисунке пунктиром, расположена ниже гидродинамической на величину скоростного напора При расчете гидравлически длинных трубопроводов, когда нет необходимости учитывать местные потери и есть уверенность, что числа Рейнольдса достаточно велики для обеспечения квадратичного сопротивления, решение существенно упрощается. Действительно, в этом случае λтр зависит только от шероховатости трубы и является для данной трубы постоянной величиной. Разрешая уравнение Дарси относительно u, имеем для расхода Q выражение
Отношение
где К – модуль расхода, или расходная характеристика – величина с размерностью расхода. Значения К для труб по ГОСТ содержатся в гидравлических справочниках (например, в [Л.4]). Уравнение (III.8) позволяет легко находить величину расхода при заданном падении напора в трубопроводе или, наоборот, напор, необходимый для обеспечения заданного расхода.
|

 Потери напора в местных сопротивлениях. В участках резкого изменения геометрии потока, там, где он сжимается, расширяется, изменяет направление, появляются обратные течения. На рис. 12 показана картина течения в элементах трубопроводной арматуры: при резком расширении трубы (а), резком сужении (б), задвижке (б), в колене (г). Появление обратных течений приводит к резкому возрастанию градиентов скорости течения внутри вихревых образований, и в соответствии с законом Ньютона для вязкого трения к росту сил трения и более интенсивному превращению механической, энергии потока в тепло.
Потери напора в местных сопротивлениях. В участках резкого изменения геометрии потока, там, где он сжимается, расширяется, изменяет направление, появляются обратные течения. На рис. 12 показана картина течения в элементах трубопроводной арматуры: при резком расширении трубы (а), резком сужении (б), задвижке (б), в колене (г). Появление обратных течений приводит к резкому возрастанию градиентов скорости течения внутри вихревых образований, и в соответствии с законом Ньютона для вязкого трения к росту сил трения и более интенсивному превращению механической, энергии потока в тепло. , (III.6)
, (III.6) ,
, . Резкое расширение – единственное из местных сопротивлений, для которого hм определяется теоретически по формуле Борда:
. Резкое расширение – единственное из местных сопротивлений, для которого hм определяется теоретически по формуле Борда: . (III.6а)
. (III.6а) ,
, .*
.* . (III.7)
. (III.7)
 , (III.7а)
, (III.7а) (III.7б)
(III.7б) , имеем
, имеем ,
, , (III.7в)
, (III.7в)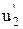 ,
,  , …,
, …,  , определяем по соответствующим им числам Рейнольдса коэффициенты трения и из формулы (III.7в) – напоры
, определяем по соответствующим им числам Рейнольдса коэффициенты трения и из формулы (III.7в) – напоры 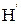 ,
,  , …,
, …,  . Построив график зависимости H = f(u2), определяем из него искомую скорость. Расход Q = u2S2.
. Построив график зависимости H = f(u2), определяем из него искомую скорость. Расход Q = u2S2. .
. .
. есть гидравлический уклон. Произведение, стоящее перед
есть гидравлический уклон. Произведение, стоящее перед  , постоянно для трубы заданного диаметра и заданной шероховатости. В итоге уравнение для расхода приобретает вид:
, постоянно для трубы заданного диаметра и заданной шероховатости. В итоге уравнение для расхода приобретает вид: , (III.8)
, (III.8)


