Дискретизация технологической информации.
5.7.1 Методы выбора интервала квантования по времени
1. На основании опытных данных (эмпирический метод) - давление – Топ = 0.5-20 сек., -температура – Топ = 5-30 с., -расход Топ = 0,1 – 1 с., -концентрация Топ = 20 – 60 с. -при известном Тоб, по формуле Топ» 0,1 * Тоб.
2. По необходимой точности. Допустим, аналоговый сигнал y(t) после квантования сигнала по времени преобразуется в сигнал y(nTоп), тогда функция ошибки Y(х)=y(t) – y(nTоп). Если допустить функцию y(t) непрерывной и дифференцируемой, разложим ёё в ряд Тэйлора на интервале (t;t+Tоп): y(t+Tоп) = y(t) +
Т.о., исследуя график изменения входного сигнала, определяют e доп и по приведенной выше формуле определяют Tоп. 3. Теорема Котельникова Для любой непрерывной функции, если она удовлетворяет условиям Дирихле (функция ограничена, непрерывна или имеет конечное число точек разрыва первого рода, имеет конечное число экстремумов), со спектром, ограниченным некоторой частотой среза
4. Метод дискретизации Железнова. Все технологические параметры делят на две основных группы: § параметры, для которых отклонения выше определенного уровня недопустимо; § параметры, для которых возможно отклонения выше определенного уровня допустимы.
Если заменить
Для параметров второй группы Топ находится по автокорреляционной функции параметра, который мы измеряем. Этот метод используется, когда Х(t) - стационарная функция. При замене непрерывного сигнала ступенчатым возникает ошибка аппроксимации, которая зависит от Топ. Поэтому возникает задача найти такой Топ, при котором среднеквадратическая ошибка аппроксимации была минимально допустимой. Дисперсия ошибки аппроксимации равняется: s2max = 2*[Кхх(0)-Кхх(t)] + sx2 изм
5.7.2 Квантование аналогового сигнала по уровню
Заключается в выделении мгновенных значений непрерывного сигнала V(t) на фиксированных дискретных уровнях в произвольные моменты времени. Фиксированные уровни сигнала обычно отстают друг от друга на постоянную величину d, называемую интервалом квантования по уровню. АЦП преобразуют аналоговый сигнал в двоичный код определенной разрядности. В зависимости от разрядности весь диапазон измерения параметра разбивается на 2n уровней. В пределах каждого такого уровня значение сигнала практически не изменяется. Задаваясь величиной подуровней d, находим число уровней квантования: m = (xmax-xmin)/d. Разрядность двоичного кода, которая используется для кодирования, имеет следующую связь с m: m = 2n – 1 Þ (xmax-xmin) /d = 2n – 1 Þ 2n = (xmax-xmin) /d+1Þ n ln2 = ln[(xmax-xmin) /d + 1] Þ d = 2*D, n = Ln (((xmax-xmin)/ (2*D)) + 1) / ln (2) = Log2(((xmax-xmin)/ (2*D)) + 1)
Пример. Найти разрядность АЦП для сигнала температуры, которая измеряется комплектом технических средств с классом точности 1, диапазон шкалы вторичного прибора 0 –1600 °С. Решение. Максимальная погрешность emax = n= Log 2 ((1600-0)/ (2*16) + 1) = 5.68» 6
|

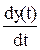 Tоп +
Tоп +  Tоп /2 + …
Tоп /2 + …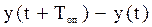 = Tоп ˑ
= Tоп ˑ 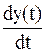

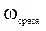 , существует интервал дискретизации, при котором можно полностью возобновить функцию по её дискретным значениям. Интервал Tоп определяют из условия, что частота опроса должна быть в два раза больше
, существует интервал дискретизации, при котором можно полностью возобновить функцию по её дискретным значениям. Интервал Tоп определяют из условия, что частота опроса должна быть в два раза больше 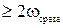
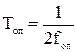 Þ
Þ  Þ
Þ  Þ
Þ 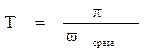
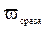 можно найти, например, по известной амплитудно-фазовой характеристике
можно найти, например, по известной амплитудно-фазовой характеристике 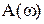
 Для параметров первой группы рекомендуется использовать методы, которые базируются на нахождении максимальной скорости изменения функции. Эти методы базируются на уравнении, которое справедливо для функций, ограниченных по модулю и имеющих конечную
Для параметров первой группы рекомендуется использовать методы, которые базируются на нахождении максимальной скорости изменения функции. Эти методы базируются на уравнении, которое справедливо для функций, ограниченных по модулю и имеющих конечную 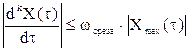
 f, а Tоп=
f, а Tоп= 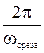 , то Топ=1/f.
, то Топ=1/f. ;
; 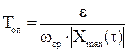
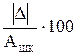 ;
; 



