Фильтрация и сглаживание
При фильтрации во временной области каждый элемент исходного сигнала заменяется последовательностью элементов, пропорциональных ему по амплитуде, но сдвинутых по времени, сумма этих элементов образует новый сигнал. Существуют различные методы фильтрации, наиболее простой реализацией отличаются методы текущего усреднения и экспоненциального сглаживания. После аналоговой фильтрации, АЦ-преобразования и ввода данных в компьютер выполняется цифровая фильтрация. Цифровая фильтрация обладает большой гибкостью, поскольку характеристики фильтра можно изменить, просто задав новые параметры соответствующей ему программы. В отличие от аналоговых, цифровые фильтры хорошо работают с длительными постоянными сигналами. В общем виде цифровой фильтр (digital filter) можно представить как
где h — это интервал выборки, ŷ;— отфильтрованный выход, а у — вход. Заметим, что аргумент kh, по смыслу представляющий из себя время, можно рассматривать и просто как номер (k) в последовательности входных значений. Если все коэффициенты ai равны нулю, то такой фильтр называется фильтром скользящего среднего (Moving Average — MA) с конечной импульсной характеристикой. Это означает, что если в течение некоторого времени все последовательные значения yi кроме одного, равны нулю, то на выходе фильтра сигнал будет отличен от нуля только на т временных интервалах. Если некоторые либо все коэффициенты ai не равны нулю, то такой фильтр называется авторегрессивным (AutoRegressive — AR) и имеет бесконечную импульсную характеристику. Другими словами, входной сигнал, отличающийся от нуля только на одном временном интервале, вызовет появление на выходе сигнала, отличного от нуля в течение бесконечно долгого времени. Обобщенный фильтр, описываемый уравнением (5.9), называется авторегрессивным фильтром скользящего среднего (AutoRegressive Moving Average — ARMA). Фильтры могут быть "причинными" и "непричинными". Причинный (causal) фильтр вычисляет выходное значение на основании ранее введенных данных (в любой момент t0 учитываются входные значения только для t < t0). Поэтому все фильтры реального времени (on-line) являются причинными. Последовательность отфильтрованных значений на выходе будет отставать на некоторое время по сравнению с последовательностью на входе. Если данные обрабатываются в автономном режиме (off-line), например при анализе серии значений уже собранных измерений, можно использовать непричинный (non-causal) фильтр. В этом случае расчет для момента времени t0 можно производить на основе как предыдущих (t < t0), так и последующих (t >t0) значений.
5.3.1. Цифровые фильтры низкой частоты Для того чтобы исследовать медленно изменяющийся входной сигнал, необходимо удалить из измерительных данных случайные пики и высокочастотные наводки, которые не содержат какой-либо полезной информации. Это можно сделать с помощью цифрового фильтра низкой частоты (digital low pass filter). Структура цифрового фильтра, который эффективно удаляет резкие колебания сигнала и в то же время не влияет на медленные изменения, всегда компромиссна, потому что частотные диапазоны исходного и постороннего сигналов обычно пересекаются. Как и у аналоговых фильтров, динамика фильтра высокого порядка более эффективна для удаления нежелательных высоких частот. Два наиболее важных типа ФНЧ — скользящего среднего и экспоненциального сглаживания (exponential smoothing). ФНЧ, используемые в промышленности, почти всегда базируются на одном из этих простых фильтров. Пример.Фильтр скользящего среднего — простейший ФНЧ. Простой фильтр скользящего среднего получается, если принять все параметры ai в уравнении (5.9) равными нулю. Если необходимо простое усреднение, то все весовые коэффициенты bi равны и дают в сумме единицу. Например, фильтр скользящего среднего с пятью входными отсчетами имеет вид
Если операция фильтрации производится не в режиме реального времени, то величину скользящего среднего можно подсчитать, используя измерения как до, так и после заданного момента времени kh. В этом случае отфильтрованное значение не отстает по времени относительно входных значений. Непричинный простой фильтр скользящего среднего по пяти значениям имеет вид
Если величина на выходе представляет собой усреднение по последним п выборкам, то она смещается на 1 + п/2 циклов. При больших значениях п выходной сигнал становится более гладким, но при этом все больше отстает по времени. Импульсная характеристика фильтра скользящего среднего конечна. Для входного импульса в момент t = 0 выходной сигнал после момента t = п становится нулевым. Скользящее среднее — это простой метод, но он имеет определенные ограничения. При использовании одинаковых коэффициентов фильтр может быть излишне инертным и недостаточно быстро реагировать на реальные изменения во входном сигнале. С другой стороны, если коэффициенты различны и убывают для больших значений индекса n, то это затрудняет анализ свойств фильтра. Экспоненциальный фильтр (exponential filter) — это авторегрессионный фильтр скользящего среднего первого порядка, определяемый следующим уравнением
Отфильтрованное значение у(kh) вычисляется суммированием предыдущего значения отфильтрованного сигнала y[(k - 1)h] и последнего значения y(kh) измерительного сигнала с весовыми коэффициентами. Коэффициент a лежит в интервале между 0 и 1. Уравнение (5.10) можно переписать в виде
т. е. экспоненциальный фильтр уточняет отфильтрованное значение на выходе сразу, как только на вход поступает новое значение. Это уточнение невелико и становится еще меньше для значений а, близких к 1; в этом случае появляется эффект инерционности. Уменьшение шумовых компонентов выходного сигнала происходит за счет слабого соответствия с реальными изменениями на входе. При а, близком к нулю, величина поправки растет. Соответственно, фильтрация шума уменьшится, однако изменения исходного сигнала будут отслеживаться более точно. При a = 0 сигнал на выходе идентичен сигналу на входе. Влияние величины а на реакцию фильтра при скачке зашумленного входного сигнала проиллюстрировано на рис. 5.2.
Рисунок 5.2 - Влияние сглаживающего экспоненциального фильтра первого порядка
Параметр а имеет значение 0, 0.5, 0.9, 0.95 и 0.98. При малых значениях а фильтр довольно точно отслеживает изменения во входном сигнале, однако сохраняется высокий уровень шума. При больших значениях а фильтр вносит значительное запаздывание, а шум заметно подавляется. При а = 0 выходной сигнал фильтра идентичен входному.
Экспоненциальный фильтр в действительности представляет собой дискретный вариант аналогового ФНЧ первого порядка с единичным статическим коэффициентом) усиления и передаточной функцией
Постоянная времени T равна R • С либо 1/R в зависимости от вида фильтра. Дифференциальное уравнение цифрового фильтра
При аппроксимации производной обратными разностями получим
что является достаточно хорошим приближением для малых значений h. Уравнение можно упростить следующим образом
что идентично уравнению (5.10) при Поскольку было принято, что h/T мало, то аппроксимация верна, только если а стремится к 1. В этом случае а можно определить следующим приближенным выражением
В действительности точное решение дифференциального уравнения (5.3.6) — это уравнение
для которого выражение (5.3.7) является хорошим приближением при малых значениях h/T. Реакция фильтра на скачок входного сигнала (рис. 5.23) иллюстрирует связь между а и Т. В течение интервала, равного одной постоянной времени Т, сигнал на выходе достигает 63 % от величины окончательного значения: при а = 0.95 постоянная времени Т равна примерно 20 интервалам выборки, а при а = 0.98 — около 50 интервалов.
Пример. Программа, реализующая экспоненциальный фильтр. Цифровой экспоненциальный фильтр [уравнение (5.10)] легко реализовать программными средствами. Ниже приведен примерный вариант программы. Функции AD_input и DA_output используются для ввода и вывода данных соответственно. Переменная delta_time есть интервал выборки, а next_time используется для синхронизации работы программы с выборкой (функция wait_until объясняется в разделе 10.6.5). program exponential_filter var in_signal, alpha: real; y_filtered, y_old: real; next_time, delta_time: real; BEGIN next_time:= 0; while true do (* бесконечный цикл *) Begin wait_until(next_time); in_signal:= AD_input (ch#l); y_filtered:= alpha*y_old + (l-alpha)*in_signal; y_old:= y_filtered; DA_output (ch#2, y_filtered); next_time:= next_time + delta_time; end; (* бесконечного цикла *) END. (* exponential_filter *)
5.3.2. Цифровые фильтры низкой частоты высоких порядков Аналоговый фильтр второго порядка более эффективен для подавления высокочастотных компонентов, чем фильтр первого порядка (раздел 5.3.2). Цифровой фильтр со структурой, определяемой уравнением (5.9), при п = т = 2 соответствует аналоговому фильтру второго порядка. Соединив последовательно два экспоненциальных фильтра первого порядка, получим фильтр второго порядка с двумя одинаковыми частотами среза
где у — значение входного сигнала, у1 — выходной сигнал первого фильтра, а у2 — выходной сигнал второго фильтра. Свойства фильтра определяются параметром а. Если исключить переменную y1(kh), то цифровой фильтр второго порядка можно записать в следующем виде
Результат применения фильтра второго порядка к сигналу, изображенному на рис. 5.2, показан на рис. 5.3. Фильтр второго порядка эффективнее подавляет высокие частоты, поэтому можно выбрать меньшее значение а. Выходной сигнал этого фильтра точнее соответствует изменениям входного сигнала, чем у фильтра первого порядка.
Рисунок 5.3 - Влияние экспоненциального фильтра второго порядка при разных значениях параметра а
Применение фильтров более высоких порядков позволяет еще больше улучшить качество выходного сигнала. Платой за это является увеличение сложности фильтра, однако стоимость обработки данных невелика. Следует отметить, что если в аналоговых фильтрах добавление пассивных электронных компонентов к цепи фильтра означает дополнительные энергетические потери в сигнале, топри программной реализации этой проблемы не существует. 5.3.3. Цифровые фильтры высокой частоты В некоторых случаях необходимо выделить высокочастотные компоненты сигналa, а не плавные изменения. Поэтому сигнал должен быть обработан фильтром высокой частоты. Разностная схема — это простой пример цифрового фильтра высокой частоты (digital high pass filter)
Выходной сигнал отличен от нуля только тогда, когда есть изменения во входном сигнале. Цифровой ФВЧ можно также получить разностной аппроксимацией аналогового ФВЧ. Соответствующее дифференциальное уравнение аналогично равнению (5.6)
де у — это входной сигнал, а у — выходной. Применив к этому уравнению аппроксимацию разностями "вперед", получим цифровой ФВЧ
где а определяется уравнением (5.12). Дискретное уравнение фильтра можно также вывести аналитически из уравнения (5.14); в результате получим а, выраженное уравнением (5.13), значение которого должно лежать между 0 и 1. При а = 0 фильтр реализует чисто разностную схему. Следует еще раз подчеркнуть, что для применения разностной аппроксимации и уравнения (5.12) отношение h/Т должно быть достаточно мало. Чувствительность фильтра на высоких частотах определяется выбором значения а. Малое значение а приводит к большей чувствительности, которая соответствует большей частоте среза для ФВЧ. Проиллюстрируем работу ФВЧ на нескольких примерах. На рис. 5.4 представлен тот же самый скачкообразный зашумленный входной сигнал рис. 5.2. Средняя диаграмма показывает выходной сигнал чистого разностного фильтра (а = 0). Она содержит пик при t = 50, так как фильтр распознает мгновенное изменение входного сигнала. Для а = 0.95 пик при t = 50 становится шире, что показано на нижней диаграмме. На рис. 5.4 на вход фильтра поступает синусоидальный сигнал с наложенным высокочастотным шумом. Выходной сигнал ФВЧ сохраняет высокочастотные изменения, а более медленные синусоидальные колебания либо уменьшены, либо удалены. Если на зашумленный синусоидальный сигнал наложить скачкообразный, то на выходе высокочастотного фильтра появится пик, отражающий скачок во входном сигнале (рис. 5.5).
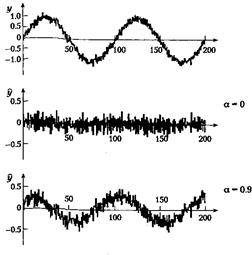
Рисунок 5.4 - Влияние фильтра высокой частоты на зашумленный синусоидальный сигнал
Рисунок 5.5 –Влияние фильтра высокой частоты первого порядка на синусоидальный сигнал. Выходной сигнал фильтра (средняя диаграмма) отслеживает только высокочастотные колебания. На нижней диаграмме показан выходной сигнал при а = 0.95 — низкочастотные компоненты присутствуют, однако с меньшей амплитудой. На верхней диаграмме показан исходный неотфильтрованный сигнал. Средняя диаграмма показывает выходной сигнал фльтра при а = 0, а нижняя диаграмма - при а = 0.95
Рисунок 5.6 Влияние фильтра высокой частоты на зашумленный синусоидальный сигнал со скачком при t = 50 (а = 0). Выходной сигнал фильтра имеет пик при. t = 50, но при этом не содержит никаких низкочастотных колебаний
|

 (5.3.4)
(5.3.4)

 (5.3.5)
(5.3.5)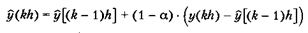






 (5.3.6)
(5.3.6)
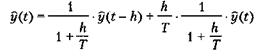
 или
или 
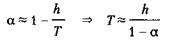 (5.3.7)
(5.3.7) (5.3.8)
(5.3.8)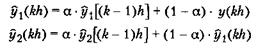



 (5.14)
(5.14) (5.15)
(5.15)