Графический способ задания функции.
Функция полностью определяется заданием пар (x; f (x)), где х пробегает все множество D (f), а y = f (x) — соответствующие значения функции — множество E (f). Множество этих пар можно записать так: Построив график отношения (произвольного), можно определить, является оно функцией или нет. Так, если каждой точке оси абсцисс соответствует не более одной точки оси ординат, то рассматриваемое отношение является функцией. Например, изображенное на рис. 2 (а) отношение является функцией, а отношение на рис. 2 (б) функцией не является, т.к. например, значению аргумента х1 соответствует два значения отношения – у1 и у2.
а) б)
Рис. 2
Сравнивая различные способы задания функции, легко установить, что недостатком аналитического способа задания функции является малая его наглядность, но по аналитическому заданию функции легко проводить ее исследование, используя математический аппарат. Часто сочетают аналитический и графический способы задания функций: по заданной формуле строится график.
|
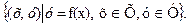Графиком функции y = f (x), 
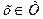называется множество пар (х,у) таких, что 
