Прямая пропорциональность, ее свойства и график
Определение. Прямой пропорциональностью называется функция,которая может быть задана при помощи формулы вида у = Прямая пропорциональность - частный случай линейной функции при в = 0 (у = К х + в Свойства функции у = 1. Область определения: Д (у) = R. 2. Множество значений: 3. Функция нечетная: f (-x) =- f(x);
Доказательство: f (-x) = К(-х) = - К х =- f(x)
4. Прямая пропорциональность: а) при К = 0 – постоянная; б) при К > 0 – возрастающая; в) при К < 0 – убывающая. Доказательство: Возьмем два значения аргумента х1 и х2 из области определения, такие, что х1 < х2, тогда х1 – х2 < 0. Запишем соответствующие им значения функции: у1 = К х1, у2 = К х2 Сравним у1 и у2: у1 – у2= Поскольку по условию х1 – х2 < 0, то знак разности у1 – у2 зависит от знака К. Если К > 0, то у1 – у2 < 0, значит у1 < у2, поэтому согласно с определением возрастающей функции, функция у = Если К < 0, то у1 – у2 >;0 5. Основное свойство прямой пропорциональности: Если задана прямая пропорциональность у = К х и две пары соответствующих значений переменных (х1; у1) и (х2; у2), то имеет место равенство:
Доказательство: Если у1 = Из равенства 6. График функции у = К х – прямая линия, проходящая через начало координат.
К > 0 К = 0 у у
К < 0 у
Примеры прямо пропорциональных зависимостей: – пройденный путь и скорость при неизменном времени; – пройденный путь и время при неизменной скорости; – количество товара и его стоимости при неизменной цене и т.д. Основное свойство прямой пропорциональности используется в школе при решении многих задач. Задача. 5 кг яблок стоят 6000 руб. Сколько стоят 8 кг таких же яблок? Решение. 1 способ: (по действиям) 1) 6000: 5 = 1200 (руб) – цена яблок 2) 1200 ∙ 8 = 9600 (руб) – стоят 8 кг яблок 2 способ: (при помощи пропорции) 5 кг – 6000 руб; 8 кг – х руб. Ответ: 9600 руб.
|

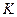 х, где х – независимая переменная, а К – действительное число.
х, где х – независимая переменная, а К – действительное число. у = К х). Говорят, что переменная у прямо пропорциональна переменной х с коэффициентом пропорциональности К. Для того, чтобы найти коэффициент пропорциональности К, достаточно знать пару соответствующих значений переменных х и у (за исключением пары (0;0)), К =
у = К х). Говорят, что переменная у прямо пропорциональна переменной х с коэффициентом пропорциональности К. Для того, чтобы найти коэффициент пропорциональности К, достаточно знать пару соответствующих значений переменных х и у (за исключением пары (0;0)), К = 

 х1 – К х2 = К(х1 – х2).
х1 – К х2 = К(х1 – х2). или у1х2 = х1у2.
или у1х2 = х1у2.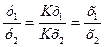 или х1у2 = х2у1.
или х1у2 = х2у1.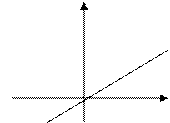 х
х  х
х

 (руб)
(руб)


