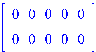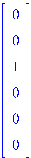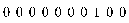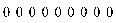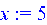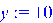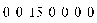Графическое представление матрицы. Вычисление определителей.
Часть 1. Задание матриц, вычисление их ранга.
Вызываем пакет "Линейная алгебра": > with(linalg);
Задаём нулевые (пустые) матрицы, определяем их тип, размерность и ранг. Знак % означает результат последней операции, %% - соответственно предпоследней. > Matrix(2);whattype(%);rank(%%);
> C:=Matrix(3,5);rank(C);
Число строк (rows). Dim – это dimension – размерность (в данном случае размер строки) > rowdim(C);
Число столбцов (columns) > coldim(C);
Другие способы задания матриц: > Matrix(1..2,1..3,8);rank(%);
> A:=Matrix([[1,2,3,4],[1,4,7,9]]);rank(%);
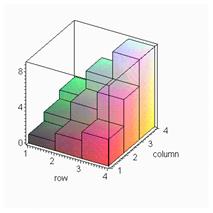
Дадим графическое представление элементов матрицы. Для этого вызовем пакет для построения графиков plots (plot– график): > with(plots): matrixplot(A,heights=histogram,axes=boxed,orientation=[-60,60]);
ЗАДАНИЯ. 1. Поясните рисунок. 2. Составьте матрицу 3х4 с двумя нулевыми и тремя отрицательными элементами и постройте её график. Поясните полученный рисунок.
> A:=Matrix(3,(i,j)->(i*j));rank(A);
Как составлена эта матрица? Вычислим миноры определителя этой матрицы:
Вычёркиваем из последней матрицы второй столбец (delcols означает delete columns – удалить столбцы) и строим полученную матрицу: > delcols(A,2..2);rank(%);with(plots): matrixplot(A,heights=histogram,axes=boxed,orientation=[-60,60]);
Вычёркиваем вторую и третью строки: > B:=delrows(A,2..3);rank(%); matrixplot(B,heights=histogram,axes=boxed,orientation=[-60,60]);
Задаём пустой вектор. По умолчанию это – вектор-столбец (column): > Vector(2);
Определяем его размерность: > vectdim(%);
Задаём вектор-строку из девяток и меняем ориентацию вектора. Теперь это вектор-строка (row): > Vector(1..7,9,orientation=row);
> vectdim(%);
Объясните следующие действия: > Vector(2,i->x*i);whattype(%);
> Vector(3,i->a^i*(b+i));
> Vector(3,i->a^(i*i)*(b-i),orientation=row);whattype(%);
> v1:=<5,7,9>;whattype(%);
> v2:=<1|3|5>;whattype(%);
Создание матрицы по строкам: > m1:=<<5|8>,<90|89>>;whattype(%);
Создание матрицы по столбцам: > m2:=<<9,6>|<08,4>>;whattype(%);
Вызываем другой пакет – LinearAlgebra. Обратите внимание, что все команды в этом пакете начинаются с заглавной буквы! > with(LinearAlgebra): Задаём единичную матрицу: > IM:=IdentityMatrix(3,3);Rank(IM);
>
> I1:=IdentityMatrix(3,9);
> matrixplot(
Нулевая матрица > ZeroMatrix(2,5);whattype(%);
Постоянная матрица. Здесь обратите внимание на различное задание квадратной и прямоугольной матриц. > ConstantMatrix(100,3);ConstantMatrix(52,3,2);
Матрица с переменными. > ScalarMatrix(a^5,2);
Единичный вектор с единицей на заданном месте. Здесь вектор – это матрица-столбец. > UnitVector(3,6);
Зададим вектор-строку с помощью опции [row]: > UnitVector[row](8,10); #Длина не больше 10
Нулевой и постоянный векторы > ZeroVector[row](9);
> ConstantVector[row](307,4);
Зададим переменные х и у и присвоим им какие-либо числовые значения. > x:=5;y:=10;
> ScalarVector[row](x+y,3,7);
Что означают цифры 3, 7 и 15?
Матрицы слишком большой размерности (>10) вычисляются, но не отображаются: > Matrix(16,16,(i,j)->i+j);
> Matrix(10,10,(i,j)->i+j);
Эта матрица отобразилась, т.к.её порядок не больше 10.
|










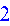



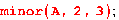
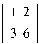



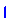




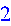
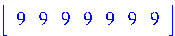


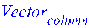

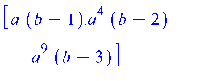





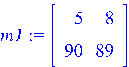







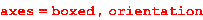
 );
);