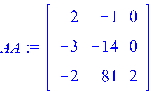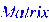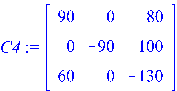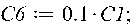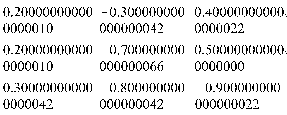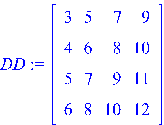Задаём квадратную матрицу
> A:=<<5,1,-1>|<-3,1,-2>|<1,1,2>>;;
Вычисляем её определитель: > det(A); Вычислим её минор, остающийся после вычёркивания 1-й строки и 2-го столбца: >
Вычислим другие миноры: >
>
Зададим другие матрицы. >
>
>
>
>
В пакете linalg так складывать матрицы нельзя. Вызовем другой пакет. > >
>
>
>
Здесь действие сложения было произведено. Сложение матрицы со скаляром равносильно сложению матрицы с диагональной матрицей, т.е. с единичной матрицей, элементы которой умножены на этот скаляр: >
Умножим матрицу на скаляр (число). >
>
Умножим матрицу на дробное число. >
Видим, что умножение матриц на дробные числа производится неправильно, т.е. в 17-м и 18-м знаках появляются какие-то цифры. Зададим матрицу не из целых, а из вещественных чисел: >
>
Результат тот же. Перемножим числа. >
Числа перемножаются правильно. Зададим квадратную матрицу. >
Прибавим к каждому элементу матрицы единицу: >
Теперь определитель отличен от нуля.
|