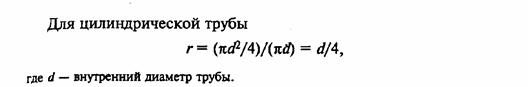ВОПРОС 2. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ ПОТОКА.

Рассмотрим зависимость между скоростями в потоке жидкости при условии неразрывности движения*.

Для этого выделим внутри потока элементарный параллелепи­пед, объем которого dV= dxdydz (рис.6). Составляющую скорос­ти вдоль оси х обозначим v _х. Тогда через левую грань параллеле­пипеда площадью dydz в него войдет за бесконечно малый проме­жуток времени масса жидкости, равная

М_х = ρv_xdydzdτ,

где р — плотность жидкости.

Примем допущение, что жидкость несжимаема. Тогда плот­ность жидкости ρ в потоке постоянна.

 

* Условие неразрывности соблюдается, когда в потоке жидкости не образуют­ся пустоты, не заполненные жидкостью.

Рис. 4.6. К выводу уравнения неразрывности потока жидкости

Равномерное движение наблюдается, когда скорость, давление, глубина и форма потока не меняются по его длине. Примером равномерного движения является движение жидкости в трубопро­воде постоянного сечения с постоянной скоростью.

Неравномерное движение происходит, например, в коничес­кой трубе, когда скорость, давление и глубина потока изменяются по длине трубы.

Если рассмотреть поперечное сечение потока жидкости и мыс­ленно представить его состоящим из отдельных элементарных струек, то окажется, что частицы жидкости, которые находятся в струйках, расположенных на различном расстоянии от оси пото­ка, движутся с различными скоростями.

Скорость движения жидкости будет максимальной по оси по­тока и минимальной в струйках у стенки трубы. Распределение скоростей в потоке зависит от режима движения жидкости.

В технике оперируют не локальными скоростями частиц жид­кости, а средней скоростью потока.

Эта скорость представляет собой отношение секундного объем­ного расхода V_ceк к площади поперечного сечения потока F:

v = V_ceк / F, (4.1.)

откуда V_ceк = vF, а массовый расход, кг/с,

 

G = ρvF,

 

где ρ — плотность жидкости, кг/м³.

 

При движении жидкости через поперечное сечение, отличное от круглого, в качестве расчетного линейного размера принимают гидравлический радиус или эквивалентный диаметр.

Гидравлический радиус вычисляют как отношение площади свободного сечения трубопровода или канала к смоченному пери­метру

r= F / П, (4.2)

где F — площадь сечения потока, м².

 

 

Рис.4.7. К выводу уравнения неразрывности потока для всего объема жидкости