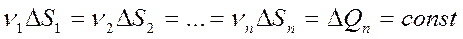Струйная модель потока
С учётом понятия средней скорости, которая во всех точках живого сечения одинакова, за единицу времени через живое сечение потока будет проходить объём жидкости (обозначим его Vtср ), равный: Vtср = SVср. Если приравнять эти объёмы Vtср = Vt=параболоида, можно определить значение средней скорости потока жидкости:
В дальнейшем среднюю скорость потока жидкости будем обозначать буквой V без индекса ср. При неравномерном движении средняя скорость в различных живых сечениях по длине потока различна. При равномерном движении средняя скорость по длине потока постоянна во всех живых сечениях. Уравнение неразрывности жидкости. В гидравлике обычно рассматривают потоки, в которых не образуются разрывы. Если выделить в потоке два любых сечения, отстоящих друг от друга на некотором расстоянии, то можно записать:
или
где Q — расход жидкости, м3/с; v — средняя скорость в сечении при установившемся движении, м/с; S— площадь живого сечения, м2 Как следует из вышерассмотренного уравнения расход, проходящий через все живые сечения потока, неизменен, несмотря на то, что в каждом сечении средняя скорость и площадь живого сечения различны. Уравнение называют уравнением неразрывности потока при установившемся движении. Из уравнения получим важное соотношение
т. е. средние скорости обратно пропорциональны площадям живых сечений, которым соответствуют эти средние скорости. Уравнение неразрывности потока — одно из основных уравнений гидродинамики. Оно выводится из уравнения неразрывности для элементарной струйки несжимаемой жидкости при установившемся движении:
где v — местные скорости в каждом живом сечении струйки, м/с; DS — площадь живого сечения элементарной струйки, м2; D Qn — элементарный расход, м3/с
Рис.- схема демонстрирующая неразрывность потока
|
В гидравлике рассматривается струйная модель движения жидкости, т.е. поток представляется как совокупность элементарных струек жидкости, имеющих различные скорости течения us. Индекс S означает (напоминает), что в каждой точке живого сечения скорости различны. Элементарные струйки как бы скользят друг по другу. Они трутся между собой и вследствие этого их скорости различаются. Причём, в середине потока скорости наибольшие, а к периферии они уменьшаются. Распределение скоростей по живому сечению потока можно представить в виде параболоида с основанием, равным S. Высота его в любой точке равна скорости соответствующей элементарной струйки uS. Площадь элементарной струйки равна dS. В пределах этой площади скорость можно считать постоянной. Понятно, что за единицу времени через живое сечение потока будет проходить объём жидкости Vt, равный объёму параболоида. Этот объём жидкости и будет равен расходу потока.
.
