Платоновы телаЯкщо вершина піраміди проектується в центр кола, яке є вписаним в основу піраміди, то центр вписаної кулі — точка перетину висоти піраміди з бісектрисою лінійного кута двогранного кута при ребрі основи.
Платоновы тела Человек проявляет интерес к правильным многоугольникам и многогранникам на протяжении всей своей сознательной деятельности – от двухлетнего ребенка, играющего деревянными кубиками, до зрелого математика. Некоторые из правильных и полуправильных тел встречаются в природе в виде кристаллов, другие – в виде вирусов, которые можно рассмотреть с помощью электронного микроскопа. Что такое правильный многогранник? Правильным называется такой многогранник, все грани которого равны (или конгруэнтны) между собой и при этом являются правильными многоугольниками. Сколько же существует правильных многогранников? На первый взгляд ответ на этот вопрос очень простой – столько же, сколько существует правильных многоугольников. Однако это не так. В «Началах Евклида» мы находим строгое доказательство того, что существует только пять выпуклых правильных многогранников, а их гранями могут быть только три типа правильных многоугольников: треугольники, квадраты и пентагоны (правильные пятиугольники). Теории многогранников посвящено много книг. Одной из наиболее известных является книга английского математика М. Венниджера «Модели многогранников». В русском переводе эта книга опубликована издательством «Мир» в 1974 г. Эпиграфом к книге выбрано высказывание Бертрана Рассела: «Математика владеет не только истиной, но и высокой красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства». Книга начинается с описания так называемых правильных многогранников, то есть многогранников, образованных простейшими правильными многоугольниками одного типа. Эти многогранники принято называть Платоновыми телами (Рис. 1), названными так в честь древнегреческого философа Платона, который использовал правильные многогранники в своей космологии.
(а)
(б) (в)
(г) (д)
Рисунок 1. Платоновы тела: (а) октаэдр («Огонь»), (б) гексаэдр или куб («Земля»), (в) октаэдр («Воздух»), (г) икосаэдр («Вода»), (д) додекаэдр («Вселенский разум») Мы начнем наше рассмотрение с правильных многогранников, гранями которых являются равносторонние треугольники. Первый из них – это тетраэдр (Рис.1-а). В тетраэдре три равносторонних треугольника встречаются в одной вершине; при этом их основания образуют новый равносторонний треугольник. Тетраэдр имеет наименьшее число граней среди Платоновых тел и является трехмерным аналогом плоского правильного треугольника, который имеет наименьшее число сторон среди правильных многоугольников. Следующее тело, которое образуется равносторонними треугольниками, называется октаэдром (Рис.1-б). В октаэдре в одной вершине встречаются четыре треугольника; в результате получается пирамида с четырехугольным основанием. Если соединить две такие пирамиды основаниями, то получится симметричное тело с восемью треугольными гранями – октаэдр. Теперь можно попробовать соединить в одной точке пять равносторонних треугольников. В результате получится фигура с 20 треугольными гранями – икосаэдр (Рис.1-г). Следующая правильная форма многоугольника – квадрат. Если соединить три квадрата в одной точке и затем добавить еще три, мы получим совершенную форму с шестью гранями, называемую гексаэдром или кубом (Рис. 1-в). Наконец, существует еще одна возможность построения правильного многогранника, основанная на использовании следующего правильного многоугольника – пентагона. Если собрать 12 пентагонов таким образом, чтобы в каждой точке встречалось три пентагона, то получим еще одно Платоново тело, называемое додекаэдром (Рис.1-д). Следующим правильным многоугольником является шестиугольник. Однако если соединить три шестиугольника в одной точке, то мы получим поверхность, то есть из шестиугольников нельзя построить объемную фигуру. Любые другие правильные многоугольники выше шестиугольника не могут образовывать тел вообще. Из этих рассуждений вытекает, что существует только пять правильных многогранников, гранями которых могут быть только равносторонние треугольники, квадраты и пентагоны. Существуют удивительные геометрические связи между всеми правильными многогранниками. Так, например, куб (Рис.1-б) и октаэдр (Рис.1-в) дуальны, т.е. получаются друг из друга, если центры тяжести граней одного принять за вершины другого и обратно. Аналогично дуальны икосаэдр (Рис.1-г) и додекаэдр (Рис.1-д). Тетраэдр (Рис.1-а) дуален сам себе. Додекаэдр получается из куба построением «крыш» на его гранях (способ Евклида), вершинами тетраэдра являются любые четыре вершины куба, попарно не смежные по ребру, то есть из куба могут быть получены все остальные правильные многогранники. Сам факт существования всего пяти действительно правильных многогранников удивителен — ведь правильных многоугольников на плоскости бесконечно много! Числовые характеристики Платоновых тел Основными числовыми характеристиками Платоновых тел является число сторон грани m, число граней, сходящихся в каждой вершине, m, число граней Г, число вершин В, число ребер Р и число плоских углов У на поверхности многогранника Эйлер открыл и доказал знаменитую формулу В — Р + Г = 2, связывающего числа вершин, ребер и граней любого выпуклого многогранника. Указанные выше числовые характеристики приведены в Табл. 1. Таблица 1 Числовые характеристики Платоновых тел
Золотая пропорция в додекаэдре и икосаэдре Додекаэдр и двойственный ему икосаэдр (Рис.1-г,д) занимают особое место среди Платоновых тел. Прежде всего необходимо подчеркнуть, что геометрия додекаэдра и икосаэдра непосредственно связана с золотой пропорцией. Действительно, гранями додекаэдра (Рис.1-д) являются пентагоны, т.е. правильные пятиугольники, основанные на золотой пропорции. Если внимательно посмотреть на икосаэдр (Рис.1-г), то можно увидеть, что в каждой его вершине сходится пять треугольников, внешние стороны которых образуют пентагон. Уже этих фактов достаточно, чтобы убедиться в том, что золотая пропорция играет существенную роль в конструкции этих двух Платоновых тел. Но существуют более глубокие математические подтверждения фундаментальной роли, которую играет золотая пропорция в икосаэдре и додекаэдре. Известно, что эти тела имеют три специфические сферы. Первая (внутренняя) сфера вписана в тело и касается его граней. Обозначим радиус этой внутренней сферы через Ri. Вторая или средняя сфера касается ее ребер. Обозначим радиус этой сферы через Rm. Наконец, третья (внешняя) сфера описана вокруг тела и проходит через его вершины. Обозначим ее радиус через Rc. В геометрии доказано, что значения радиусов указанных сфер для додекаэдра и икосаэдра, имеющего ребро единичной длины, выражается через золотую пропорцию t (Табл.2). Таблица 2 Золотая пропорция в сферах додекаэдра и икосаэдра
Заметим, что отношение радиусов В геометрии известны и другие соотношения для додекаэдра и икосаэдра, подтверждающие их связь с золотой пропорцией. Например, если взять икосаэдр и додекаэдр с длиной ребра, равной единице, и вычислить их внешнюю площадь и объем, то они выражаются через золотую пропорцию (Табл.3). Таблица 3 Золотая пропорция во внешней площади и объеме додекаэдра и икосаэдра
Таким образом, существует огромное количество соотношений, полученных еще античными математиками, подтверждающих замечательный факт, что именно золотая пропорция является главной пропорцией додекаэдра и икосаэдра, и этот факт является особенно интересным с точки зрения так называемой «додекаэдро-икосаэдрической доктрины», которую мы рассмотрим ниже. Космология Платона Рассмотренные выше правильные многогранники получили название Платоновых тел, так как они занимали важное место в философской концепции Платона об устройстве мироздания.
Платон (427-347 годы до н.э.) Четыре многогранника олицетворяли в ней четыре сущности или «стихии». Тетраэдр символизировал Огонь, так как его вершина устремлена вверх; Икосаэдр — Воду, так как он самый «обтекаемый» многогранник; Куб — Землю, как самый «устойчивый» многогранник; Октаэдр — Воздух, как самый «воздушный» многогранник. Пятый многогранник, Додекаэдр, воплощал в себе «все сущее», «Вселенский разум», символизировал все мироздание и считался главной геометрической фигурой мироздания. Гармоничные отношения древние греки считали основой мироздания, поэтому четыре стихии у них были связаны такой пропорцией: земля/вода = воздух/огонь. Атомы «стихий» настраивались Платоном в совершенных консонансах, как четыре струны лиры. Напомним, что консонансом называется приятное созвучие. В связи с этими телами уместно будет сказать, что такая система элементов, включавшая четыре элемента — землю, воду, воздух и огонь, — была канонизирована Аристотелем. Эти элементы оставались четырьмя краеугольными камнями мироздания в течение многих веков. Вполне возможно отождествить их с известными нам четырьмя состояниями вещества — твердым, жидким, газообразным и плазменным. Таким образом, представление о «сквозной» гармонии бытия древние греки связывали с ее воплощением в Платоновых телах. Влияние знаменитого греческого мыслителя Платона сказалось и на Началах Евклида. В этой книге, которая на протяжении веков была единственным учебником геометрии, дано описание «идеальных» линий и «идеальных» фигур. Самая «идеальная» линия – прямая, а самый «идеальный» многоугольник – правильный многоугольник, имеющий равные стороны и равные углы. Простейшим правильным многоугольником можно считать равносторонний треугольник, поскольку он имеет наименьшее число сторон, которое может ограничивать часть плоскости. Интересно, что Начала Евклида начинаются описанием построения правильного треугольника и заканчиваются изучением пяти Платоновых тел. Заметим, что Платоновым телам посвящена заключительная, то есть, 13-я книга Начал Евклида. Кстати, этот факт, то есть размещение теории правильных многогранников в заключительной (то есть как бы самой главной) книге Начал Евклида, дало основание древнегреческому математику Проклу, который был комментатором Евклида, выдвинуть интересную гипотезу об истинных целях, которые преследовал Евклид, создавая свои Начала. Согласно Проклу, Евклид создавал Начала не с целью изложения геометрии как таковой, а чтобы дать полную систематизированную теорию построения «идеальных» фигур, в частности пяти Платоновых тел, попутно осветив некоторые новейшие достижения математики! Не случайно, что один из авторов открытия фуллеренов, Нобелевский лауреат Гарольд Крото в свой Нобелевской лекции начинает свой рассказ о симметрии как «основе нашего восприятия физического мира» и ее «роли в попытках его всестороннего объяснения» именно с Платоновых тел и «элементов всего сущего»: «Понятие структурной симметрии восходит к античной древности...» Наиболее известные примеры можно, конечно, обнаружить в диалоге «Тимей» Платона, где в разделе 53, относящемся к «Элементам», он пишет: «Во-первых, каждому (!), разумеется, ясно, что огонь и земля, вода и воздух суть тела, а всякое тело — сплошное» (!!) Платон обсуждает проблемы химии на языке этих четырех элементов и связывает их с четырьмя Платоновыми телами (в то время только четырьмя, пока Гиппарх не открыл пятый — додекаэдр). Хотя на первый взгляд такая философия может показаться несколько наивной, она указывает на глубокое понимание того, каким образом в действительности функционирует Природа».
|
; 
; 
.
— лінійний кут двогранного кута між площиною бічної грані CSB і площиною основи;
;
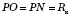— радіус кулі;
або 
, де l — довжина апофеми.
;
або 
. 
.
= 
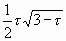
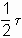
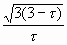одинаково, как для икосаэдра, так и для додекаэдра. Таким образом, если додекаэдр и икосаэдр имеют одинаковые вписанные сферы, то их описанные сферы также равны между собой. Доказательство этого математического результата дано в Началах Евклида.
