Распределение обуви, проданной коммерческой фирмой в январе 2008г.

1.

 

2.

 

3.

 

 

 

 

4.

 

 

 

 

5.

 

 

 

ХАРАКТЕРИСТИКИ ВАРИАЦИОННОГО РЯДА. СТРУКТУРНЫЕ СРЕДНИЕ

Мода – значение признака, наиболее часто встречающегося в исследуемой совокупности.

Медиана – значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.

Для дискретных вариационных рядов модой будет значение варианта с наибольшей частотой. Вычисление медианы в дискретных рядах распределения имеет специфику. Если такой ряд распределения имеет нечётное число членов, то медианой будет вариант, находящийся в середине ранжированного ряда. Если ранжированный ряд распределения состоит из чётного числа членов, то медианой будет средняя арифметическая из двух значений признака, расположенных в середине ряда.

Пример. Рассчитаем моду и медиану по данным табл. 7.10.

Т а б л и ц а 7.10.

Распределение обуви, проданной коммерческой фирмой в январе 2008г.

Размер

Me

42 Mo

44 и более

Итого

Количество проданных пар, % к итогу

Накопленные частоты

-

В этом ряду распределения мода равна 42. Именно этот размер обуви в январе 2008 г. пользовался наибольшим спросом.

Для определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание продолжается до получения накопленной суммы частот, впервые превышающей половину. В нашем примере сумма частот составила 100, её половина – 50. Накопленная сумма частот ряда равна 62. Ей соответствует значение признака равное 40. Таким образом, 40-й размер обуви является медианным.

Для интервальных вариационных рядов мода определяется по формуле:

где x_Mo – нижняя граница значения интервала, содержащего моду;

i_Mo – величина модального интервала;

f_Mo – частота модального интервала;

f_Mo–1 – частота интервала, предшествующего модальному;

f_Mo+1 – частота интервала, следующего за модальным.

Медиана интервального ряда распределения определяется по формуле:

,

где x_Me – нижняя граница значения интервала, содержащего медиану;

i_Me – величина медианного интервала;

∑f – сумма частот;

S_Me-1 – сумма накопленных частот, предшествующих медианному интервалу;
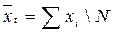