Моменты распределения
Для характеристики вариационных рядов используют начальные и центральные моменты k-того порядка. Начальные моменты обозначаются через m:
Тогда начальный момент первого порядка:
начальный момент второго порядка:
начальный момент третьего порядка: И т. д. Практически при анализе вариационных рядов ограничиваются расчётом моментов первых четырёх порядков. Центральные моменты обозначаются через mk, можно записать в общем виде:
а моменты первых четырёх порядков в виде:
;. Как видно из записанных формул, центральный момент второго порядка представляет собой не что иное, как дисперсию. Центральный момент третьего порядка (m3) используется для характеристики асимметричности распределения, ибо для симметричных рядов всегда:
Момент k-того порядка mk – это средняя арифметическая k-й степени отклонений отдельных вариантов от какой-то велечины.
|
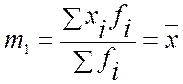(средняя арифметическая);
;
,
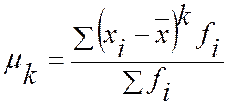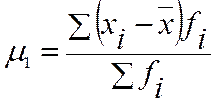=0; 
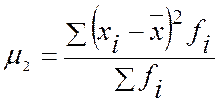=s2;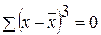
.
