Теорема Лапласа разложения определителя.
Пусть Определение. Минором k-го порядка матрицы называется определитель матрицы, составленной из элементов некоторых ее k строк и k столбцов ( Пример. Рассмотрим матрицу Миноры первого порядка – это в точности элементы матрицы, а значит, их число равно 12. Вычислим миноры второго порядка. Например, если выбрать две первые строки, то минорами второго порядка будут определители Миноры третьего порядка – это определители, составленные из элементов первых трех строк: Миноры матрицы используют для вычисления ее ранга. Теорема (без доказательства) Ранг матрицы равен наивысшему порядку ее миноров, отличных от нуля. На этом утверждении основан так называемый метод окаймляющих миноров вычисления ранга матрицы. Если все элементы матрицы равны нулю, т.е. матрица нулевая, то ее ранг равен нулю. Пусть матрица ненулевая. Выберем ненулевой минор первого порядка и перебираем миноры второго порядка, которые содержат это минор. Если все такие миноры окажутся равными нулю, то ранг матрицы равен 1. Если найдется ненулевой минор второго порядка, то окаймляем его минорами третьего порядка до тех пор, пока не найдем ненулевой. Если все миноры третьего порядка окажутся равными нулю, то ранг матрицы равен 2. Этот процесс перебираем до тех пор, пока не получим на некотором шаге все нулевые миноры, либо пока не переберем всевозможные миноры матрицы. Пример. Ранг рассмотренной матрицы равен двум, так как все ее миноры третьего порядка нулевые (убедитесь в этом самостоятельно). Если матрица квадратная, то можно ввести понятия дополнительного минора и алгебраического дополнения минора k –го порядка. Определение. Дополнительным минором минора k-го порядка квадратной матрицы называется определитель матрицы, полученной вычеркиванием выбранных k строк и k столбцов. Очевидно, что дополнительный минор минора k -го порядка является минором порядка n-k. Определение. Алгебраическим дополнением минора k-го порядка квадратной матрицы называется число, равное произведению дополнительного минора на -1 в степени, равной сумме номеров выбранных строк и столбцов. Пример. Теорема 2 (теорема Лапласа) Пусть в матрице выбрано k строк. Тогда ее определитель равен сумме произведений всех миноров k -го порядка, составленных из элементов выбранных строк, и их алгебраических дополнений. Без доказательства. Пример.
|

 – матрица размерности m на n.
– матрица размерности m на n.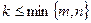 ).
).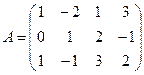 . Для этой матрицы можно вычислить миноры первого, второго и третьего порядков.
. Для этой матрицы можно вычислить миноры первого, второго и третьего порядков.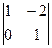 ,
,  ,
,  ,
,  и т.д. Для вычисления миноров второго порядка можно было выбрать первую и последнюю строки, вторую и последнюю строки.
и т.д. Для вычисления миноров второго порядка можно было выбрать первую и последнюю строки, вторую и последнюю строки. ,
,  и т.д.
и т.д.


