4. 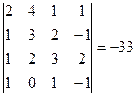
5. 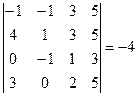
6. 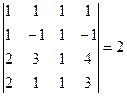
7. 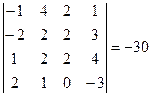
8. 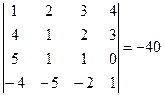
9. 
10. 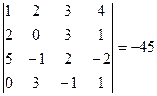
11. 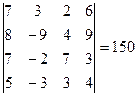
12. 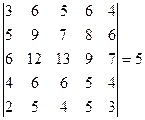
13. 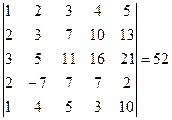
14. 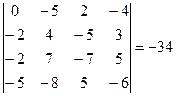
15. 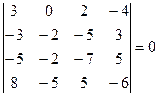
16. 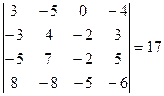
17. 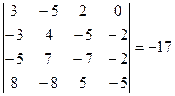
Определитель произведения матриц.
Теорема. Определитель произведения матриц равен произведению определителей этих матриц: 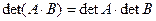
Доказательство разобьем на несколько случаев.
Случай 1. Пусть  – элементарная матрица n -го порядка, т.е. получена из единичной одним из элементарных преобразований. По свойствам определителей,
– элементарная матрица n -го порядка, т.е. получена из единичной одним из элементарных преобразований. По свойствам определителей,  . По свойствам элементарных матриц матрицу
. По свойствам элементарных матриц матрицу  можно получить из матрицы B тем же элементарным преобразованием, поэтому
можно получить из матрицы B тем же элементарным преобразованием, поэтому  . Таким образом, в этом случае
. Таким образом, в этом случае 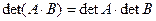 .
.
Случай 2. Покажем, что утверждение верно для произведения любого числа элементарных матриц:  . Доказательство проведем, используя метод математической индукции:
. Доказательство проведем, используя метод математической индукции:
а)  верно в силу случая 1.
верно в силу случая 1.
б) Пусть утверждение верно для k множителей. Покажем, что тогда оно верно и для k+1 множителей.
 .
.
Случай 3. Пусть теперь A и B – произвольные матрицы n -го порядка.
Если 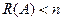 , то
, то  . По теореме о столбцовом пространстве произведения матриц
. По теореме о столбцовом пространстве произведения матриц  . Поэтому
. Поэтому  , а значит,
, а значит,  .
.
Аналогично, если  , то
, то 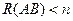 , а значит,
, а значит, 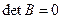 и
и  .
.
Пусть теперь  , т.е. обе матрицы невырожденные. Следовательно, по свойствам элементарных матриц, каждую из них можно представить в виде произведения элементарных матриц. Таким образом, применяя случай 2,
, т.е. обе матрицы невырожденные. Следовательно, по свойствам элементарных матриц, каждую из них можно представить в виде произведения элементарных матриц. Таким образом, применяя случай 2,  и
и  ■
■

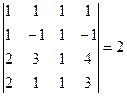
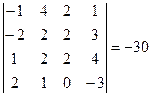
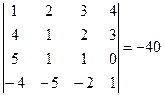

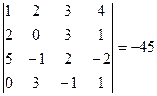
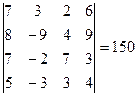
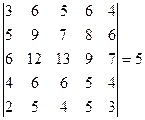
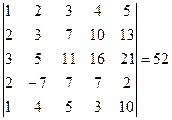
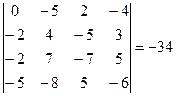
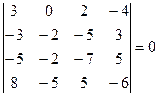
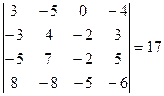
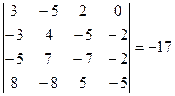
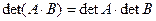
 – элементарная матрица n -го порядка, т.е. получена из единичной одним из элементарных преобразований. По свойствам определителей,
– элементарная матрица n -го порядка, т.е. получена из единичной одним из элементарных преобразований. По свойствам определителей,  . По свойствам элементарных матриц матрицу
. По свойствам элементарных матриц матрицу  можно получить из матрицы B тем же элементарным преобразованием, поэтому
можно получить из матрицы B тем же элементарным преобразованием, поэтому  . Таким образом, в этом случае
. Таким образом, в этом случае  . Доказательство проведем, используя метод математической индукции:
. Доказательство проведем, используя метод математической индукции: верно в силу случая 1.
верно в силу случая 1. .
.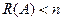 , то
, то  . По теореме о столбцовом пространстве произведения матриц
. По теореме о столбцовом пространстве произведения матриц  . Поэтому
. Поэтому  , а значит,
, а значит,  .
. , то
, то 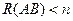 , а значит,
, а значит, 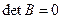 и
и  , т.е. обе матрицы невырожденные. Следовательно, по свойствам элементарных матриц, каждую из них можно представить в виде произведения элементарных матриц. Таким образом, применяя случай 2,
, т.е. обе матрицы невырожденные. Следовательно, по свойствам элементарных матриц, каждую из них можно представить в виде произведения элементарных матриц. Таким образом, применяя случай 2,  и
и  ■
■


