Тест N 1
Уважаемые студенты!
В соответствии с программой курса высшей математики в первом семестре для вас подготовлены 5 контрольных работ «Проверь себя» (с ответами). Выполнение этих работ будет хорошей подготовкой к текущим и экзаменационному тестам по высшей математике.
| 1. Линейная алгебра
| | Условия задач
| Ответы
| |
| Вычислить:  . .
| – 10
| |
| Вычислить:  . .
| – 1
| |
| Дана система уравнений  Найти Найти  . .
| 
| |
| Решить систему уравнений, приняв в качестве базисных переменных  и и  : :
 . .
| 
| |
| 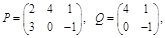  .
Какие произведения существуют? Указать все случаи.
А) .
Какие произведения существуют? Указать все случаи.
А)  ; Б) ; Б)  ; В) ; В)  ; Г) ; Г)  ; Д) ; Д)  ; Е) ; Е)  . .
| Б, В
| |
| Вычислить:  . .
| 
| |
| Какие матрицы имеют обратные? Указать все случаи.
А)  ; Б) ; Б)  ; В) ; В) 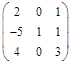 ; Г) ; Г)  . .
| А,В
| |
| 
| 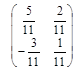
| |
| 
| 
| |
| Найти ранг матрицы  . .
|
| |
| Какие матрицы имеют ранг, равный 2? Указать все случаи.
А=  ; Б= ; Б=  ; В= ; В=  ; Г= ; Г=  . .
| Б,Г
| |
| Пусть система п линейных уравнений содержит k неизвестных, A - матрица коэффициентов при неизвестных, B - расширенная матрица. Выбрать все верные утверждения: cистема уравнений имеет единственное решение, если
А) rang А < rang В; Б) rang А = rang В = k;В) rang А = rang В = n; Г) rang А = rang В; Д) rang А = rang В < k.
|
Б
| |
| Указать все верные утверждения: если ранг матрицы равен k, то
А) все миноры порядка k не равны 0;
Б) равны нулю все миноры порядка < k;
В) равны нулю все миноры порядка > k.
| В
|
| 2. Векторная алгебра
| | Условия задач
| Ответы
| |
| Найти орт вектора  . .
| 
| |
| Вектор составляет с координатными осями Ox и Oz углы  , а с осью Oy – острый угол , а с осью Oy – острый угол  . Найти . Найти  . .
| 
| |
| Вектор  параллелен вектору параллелен вектору  . Найти . Найти  . .
|
| |
| Векторы  и и  образуют угол образуют угол  . Найти . Найти  , если , если   . .
| 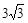
| |
| 
|
| |
| Вычислить  , если , если 
| –19
| |
|  . Найти . Найти 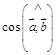 . .
| 
| |
| Определить  , при котором ортогональны векторы , при котором ортогональны векторы  и и  . .
|
| |
| Найти  , если , если 
| 1,2
| |
| Вычислить  , если , если  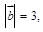 а угол между векторами а угол между векторами  и и  равен равен  . .
|
| |
| Векторы  и и 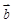 образуют угол образуют угол  . Зная, что . Зная, что  , найти , найти 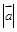 . .
| 
| |
| Вычислить  . .
| 
| |
| Найти площадь параллелограмма, построенного на векторах 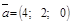 и и  , как на сторонах. , как на сторонах.
|
| |
| Найти площадь треугольника с вершинами в точках А(1;1;1), В(4;0;1), С(2;3;1).
| 3,5
| |
| Вычислить смешанное произведение  если если   , ,  . .
| – 18
| |
| Найти объем параллелепипеда, построенного на векторах 
|
| |
| Найти объем треугольной пирамиды с вершинами в точках
 , ,  , , 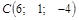 , ,  . .
|
| |
| Определить, при каком  компланарны векторы компланарны векторы 
| 
| |
| Какие равенства верны? Указать все варианты.
А)  ; Б) ; Б)  ; В) ; В)  . .
| А,Б
| |
| Какие равенства верны? Указать все варианты.
А)  ; Б) ; Б)  ; В) ; В)  ; Г) ; Г)  ; Д) ; Д)  . .
| В,Д
| |
| Площадь параллелограмма, построенного на векторах  и и  , как на сторонах, равна
А) , как на сторонах, равна
А)  ; Б) ; Б)  ; В) ; В)  ; Г) ; Г)  ; Д) ; Д) 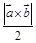 . .
| Б
| |
| Какие величины являются векторами? Указать все варианты.
А) 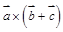 ; Б) ; Б)  ; В) ; В)  . .
| А
| |
| Если ненулевые векторы 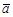 и и 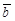 параллельны друг другу, то (указать все верные утверждения): А) параллельны друг другу, то (указать все верные утверждения): А)  =0; Б) =0; Б)  =0; В) =0; В)  ; Г) ; Г)  . .
| А,В
| |
| Если три вектора  компланарны, то (указать все варианты)
А) компланарны, то (указать все варианты)
А) 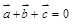 ; Б) ; Б)  ; В) ; В)  ; Г) ; Г)  ; Д) ; Д)  . .
| В,Г
| |
| Если вектор 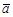 ортогонален вектору ортогонален вектору 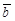 , то (указать все верные утверждения):
А) , то (указать все верные утверждения):
А)  =0; Б) =0; Б)  ; В) ; В)  ; Г) ; Г)  =0. =0.
| А,Б
|
| 3. Аналитическая геометрия
| | Условия задач
| Ответы
| |
| Составить уравнение плоскости проходящей через точки    . .
| 
| |
| Нормаль к плоскости, проходящей через точки A (1;1;4), B (1;4;1), C (−1;1;5), может иметь вид
| (1; 2; 2)
| |
| Составить уравнение плоскости, проходящей через точку  параллельно плоскости параллельно плоскости  . .
| 
| |
| Составить уравнение плоскости, проходящей через точку  перпендикулярно прямой перпендикулярно прямой  . .
| 
| |
| Если  острый угол между плоскостями 3 x - 2 y + z - 5 = 0 и 2 x - y + 3 z +7 = 0, то острый угол между плоскостями 3 x - 2 y + z - 5 = 0 и 2 x - y + 3 z +7 = 0, то
| 
| |
| Если плоскость 5 x + By + z - 1 = 0 параллельна плоскости 3 x - y + Cz +4 = 0, то В+С=
| 
| |
| Найти расстояние от точки М (5;-1;3) до плоскости 2 x−y+ 2 z +1=0.
|
| |
| Составить уравнение плоскости, проходящей через точку  перпендикулярно плоскостям перпендикулярно плоскостям  и и  . .
| 
| |
| Составить уравнение плоскости, проходящей через точки  и и  параллельно вектору параллельно вектору 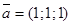 . .
| 
| |
| Уравнение прямой, проходящей через точки  и и  , может иметь вид , может иметь вид
| 
| |
| Составить уравнение прямой, проходящей через точку 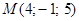 параллельно прямой параллельно прямой  . .
| 
| |
| Составить уравнение прямой, проходящей через точку  перпендикулярно плоскости перпендикулярно плоскости 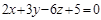 . .
| 
| |
| Если прямая 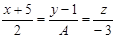 параллельна прямой параллельна прямой  , то , то 
|
| |
| Определить, при каком  перпендикулярны прямые: перпендикулярны прямые:
 и и  . .
|
| |
| Если  острый угол между прямой острый угол между прямой  и плоскостью и плоскостью 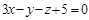 , то , то
| 
| |
| Определить, при каком С прямая  параллельна плоскости параллельна плоскости  . .
| – 2
| |
| Направляющий вектор прямой пересечения двух плоскостей  может иметь координаты
может иметь координаты
| (1;-3;2)
| |
| Найти точку пересечения прямой  и плоскости и плоскости  . .
| (0;8;-4)
| |
| Найти все пары векторов, образующих базис:
А)  ; Б) ; Б)  ; В) ; В)  ; Г) ; Г)  . .
| А,Б, Г
| |
| Определить  , при котором векторы , при котором векторы  и и  не образуют базис. не образуют базис.
| – 0,8
| |
| Разложить вектор  по базису по базису   . .
| 
| |
| Найти максимальное из собственных значений матрицы  . .
|
| |
| Составить уравнение эллипса, фокусы которого лежат на оси абсцисс симметрично относительно начала координат, если если малая полуось b = 4, а c = 2.
| 
| |
| Найти эксцентриситет эллипса 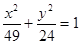 . .
| 
| |
| Центр эллипса  находится в точке находится в точке
| (2; - 1)
| |
| Найти радиус окружности  . .
| 
| |
| Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, если действительная полуось  . .
| 
| |
| Уравнения асимптот гиперболы  имеют вид имеют вид
| 
| |
| Центр гиперболы  находится в точке находится в точке
| (3; -1)
| |
| Составить уравнение параболы, если даны ее фокус  и директриса и директриса  . .
| 
| |
| Вершина параболы  находится в точке находится в точке
| (–1; 2)
| |
| Определить вид и расположение кривой  . .
| Гипербола с центром в точке
(4; –1)
| |
| Указать все верные утверждения:
А)  - уравнение цилиндра;
Б) - уравнение цилиндра;
Б) 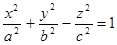 - уравнение конуса;
В) - уравнение конуса;
В)  - уравнение однополостного гиперболоида;
Г) - уравнение однополостного гиперболоида;
Г) 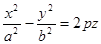 - уравнение гиперболического параболоида. - уравнение гиперболического параболоида.
| Г
| |
| Указать все верные утверждения:
если  - оператор, сопряженный к - оператор, сопряженный к  , а , а  - к - к 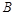 , то
А) , то
А)  ; Б) ; Б)  ;
В) ;
В)  ; Г) ; Г)  . .
| А,Б
| |
| В результате приведения к каноническому виду получена некоторая кривая. Выберите все верные утверждения: если кривая
А) гипербола, то  ;
Б) эллипс, то ;
Б) эллипс, то  ;
В) парабола, то ;
В) парабола, то  .
(Здесь .
(Здесь  и и  - собственные значения матрицы квадратичной формы.) - собственные значения матрицы квадратичной формы.)
| Б,В
| |
| Выбрать все верные утверждения:
А) Если векторы линейно независимы, то они образуют базис.
Б) Если векторы образуют базис, то они линейно независимы.
В) Для того, чтобы векторы образовывали базис, необходимо и достаточно, чтобы они были линейно независимыми.
Г) Если векторы линейно зависимы, они не образуют базис.
| Б,Г
| |
| Пусть заданы m векторов n – мерного пространства.
Указать все правильные утверждения:
А) Если m > n, то векторы не образуют базис.
Б) Если m < n, то векторы образуют базис.
В) Если m > n, то векторы линейно зависимы.
Г) Если m = n, то векторы образуют базис.
| А,В
|
| 4. Пределы
| | Условия задач
| Ответы
| |
| 
| 
| |
| 
| 
| |
| 
|
| |
| 
| – 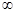
| |
| 
| 
| |
| 
| 
| |
| 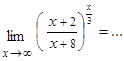
| 
| |
| 
| 
| |
| 
|
| |
| 
| 
| |
| 
| 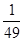
| |
| Утверждение  означает, что
А) означает, что
А)  ;
Б) ;
Б)  ;
В) ;
В)  ;
Г) ;
Г) 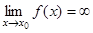 ;
Д) ;
Д)  . .
| Д
| |
| Выбрать правильные утверждения:
А) Произведение бесконечно малой на ограниченную величину есть бесконечно малая.
Б) Произведение бесконечно большой на ограниченную величину есть величина ограниченная.
В) Произведение конечного числа бесконечно малых величин есть бесконечно малая.
Г) Сумма бесконечно малых величин есть бесконечно малая.
| А,В
|
| 5. Производные
| | Условия задач
| Ответы
| |
| Найти  , если , если  . .
| 
| |
| Найти  , если , если 
| 
| |
| Для функции  найти найти  . .
| 
| |
| Для функции  найти найти  . .
| 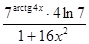
| |
| Для функции  найти найти  в точке М (1;1). в точке М (1;1).
| 9 и 2,5
| |
| Найти 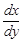 , если , если 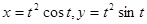 . .
| 
| |
| Найти  , если , если  . .
| 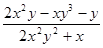
| |
| Дана функция  , где , где  . Найти . Найти 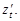
| 
| |
| Дана функция 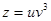 , где , где  Найти Найти 
|
| |
| Найти невертикальные асимптоты кривой  . .
| 
| |
| Исследовать на непрерывность функцию  в точках x =2 и x =5. в точках x =2 и x =5.
| х = 2 скачок
х = 5 точка непрер.
| |
| Исследовать на непрерывность функцию  в точках в точках  и и  . .
| x = 5-разрыв II рода
х = 6-точка непрер.
| |
| Найти интервал(ы) убывания функции  . .
| (0;1)
| |
| Найти интервал(ы) выпуклости функции  . .
| 
| |
| Найти экстремум функции z = xy+ 3 x, если x+ y −5 = 0.
| zmax(4;1)=16
| |
| Исследовать на экстремум функцию z = 2 x 3-3 y 2+6 xy в точках A (0;0) и B (−1;−1).
| А – нет экстремума
В – точка максимума
| |
| Найти производную функции z = x 2 y в точке М (2;3) в направлении вектора 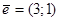 . .
| 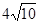
| |
| Найти наибольшую скорость возрастания функции z = x 3 y +2 y ² в точке M (1;1).
| 
| |
| Если кривая выпукла и возрастает на отрезке 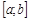 , то для , то для  А)
А) 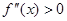 , ,  ; Б) ; Б)  , , 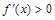 ;
В) ;
В) 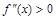 , , 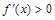 ; Г) ; Г)  , ,  ;
Д) ;
Д) 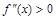 , ,  . .
| Б
|
Тест N 1

Шрифт зодчего Шрифт зодчего состоит из прописных (заглавных), строчных букв и цифр...
|

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|
Роль органов чувств в ориентировке слепых Процесс ориентации протекает на основе совместной, интегративной деятельности сохранных анализаторов, каждый из которых при определенных объективных условиях может выступать как ведущий...
Лечебно-охранительный режим, его элементы и значение.
Терапевтическое воздействие на пациента подразумевает не только использование всех видов лечения, но и применение лечебно-охранительного режима – соблюдение условий поведения, способствующих выздоровлению...
Тема: Кинематика поступательного и вращательного движения. 1. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется со временем
1. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью...
|
Билет №7 (1 вопрос) Язык как средство общения и форма существования национальной культуры. Русский литературный язык как нормированная и обработанная форма общенародного языка Важнейшая функция языка - коммуникативная функция, т.е. функция общения Язык представлен в двух своих разновидностях...
Патристика и схоластика как этап в средневековой философии Основной задачей теологии является толкование Священного писания, доказательство существования Бога и формулировка догматов Церкви...
Основные симптомы при заболеваниях органов кровообращения При болезнях органов кровообращения больные могут предъявлять различные жалобы: боли в области сердца и за грудиной, одышка, сердцебиение, перебои в сердце, удушье, отеки, цианоз головная боль, увеличение печени, слабость...
|
|

 .
.
 .
.
 Найти
Найти  .
.

 и
и  :
:
 .
.

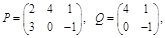
 .
Какие произведения существуют? Указать все случаи.
А)
.
Какие произведения существуют? Указать все случаи.
А)  ; Б)
; Б)  ; В)
; В)  ; Г)
; Г)  ; Д)
; Д)  ; Е)
; Е)  .
.
 .
.

 ; Б)
; Б)  ; В)
; В) 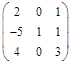 ; Г)
; Г)  .
.

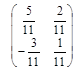


 .
.
 ; Б=
; Б=  ; В=
; В=  ; Г=
; Г=  .
.
 .
.

 , а с осью Oy – острый угол
, а с осью Oy – острый угол  . Найти
. Найти 
 параллелен вектору
параллелен вектору  . Найти
. Найти  .
.
 и
и  образуют угол
образуют угол  . Найти
. Найти  , если
, если 
 .
.
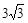

 , если
, если 
 . Найти
. Найти 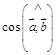 .
.

 , при котором ортогональны векторы
, при котором ортогональны векторы  и
и  .
.
 , если
, если 
 , если
, если 
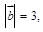 а угол между векторами
а угол между векторами  и
и  .
.
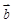 образуют угол
образуют угол  . Зная, что
. Зная, что  , найти
, найти 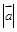 .
.

 .
.

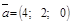 и
и  , как на сторонах.
, как на сторонах.
 если
если 
 ,
,  .
.

 ,
,  ,
, 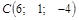 ,
,  .
.


 ; Б)
; Б)  ; В)
; В)  .
.
 ; Б)
; Б)  ; В)
; В)  ; Г)
; Г)  ; Д)
; Д)  .
.
 ; Б)
; Б)  ; В)
; В)  ; Г)
; Г) 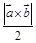 .
.
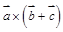 ; Б)
; Б)  ; В)
; В)  .
.
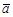 и
и 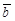 параллельны друг другу, то (указать все верные утверждения): А)
параллельны друг другу, то (указать все верные утверждения): А)  ; Г)
; Г)  .
.
 компланарны, то (указать все варианты)
А)
компланарны, то (указать все варианты)
А) 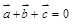 ; Б)
; Б)  ; В)
; В)  ; Г)
; Г)  ; Д)
; Д)  .
.


 .
.

 параллельно плоскости
параллельно плоскости  .
.

 перпендикулярно прямой
перпендикулярно прямой  .
.

 острый угол между плоскостями 3 x - 2 y + z - 5 = 0 и 2 x - y + 3 z +7 = 0, то
острый угол между плоскостями 3 x - 2 y + z - 5 = 0 и 2 x - y + 3 z +7 = 0, то


 перпендикулярно плоскостям
перпендикулярно плоскостям  и
и  .
.

 и
и  параллельно вектору
параллельно вектору 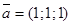 .
.

 и
и  , может иметь вид
, может иметь вид

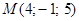 параллельно прямой
параллельно прямой  .
.

 перпендикулярно плоскости
перпендикулярно плоскости 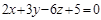 .
.

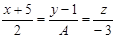 параллельна прямой
параллельна прямой  , то
, то 
 и
и  .
.
 и плоскостью
и плоскостью 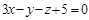 , то
, то

 параллельна плоскости
параллельна плоскости  .
.
 может иметь координаты
может иметь координаты
 и плоскости
и плоскости  .
.
 ; Б)
; Б)  ; В)
; В)  ; Г)
; Г)  .
.
 , при котором векторы
, при котором векторы  и
и  не образуют базис.
не образуют базис.
 по базису
по базису 
 .
.

 .
.

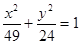 .
.

 находится в точке
находится в точке
 .
.

 .
.

 имеют вид
имеют вид

 находится в точке
находится в точке
 и директриса
и директриса  .
.

 находится в точке
находится в точке
 .
.
 - уравнение цилиндра;
Б)
- уравнение цилиндра;
Б) 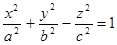 - уравнение конуса;
В)
- уравнение конуса;
В)  - уравнение однополостного гиперболоида;
Г)
- уравнение однополостного гиперболоида;
Г) 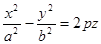 - уравнение гиперболического параболоида.
- уравнение гиперболического параболоида.
 - оператор, сопряженный к
- оператор, сопряженный к  , а
, а  - к
- к 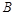 , то
А)
, то
А)  ; Б)
; Б)  ;
В)
;
В)  ; Г)
; Г)  .
.
 ;
Б) эллипс, то
;
Б) эллипс, то  .
(Здесь
.
(Здесь  и
и  - собственные значения матрицы квадратичной формы.)
- собственные значения матрицы квадратичной формы.)






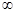




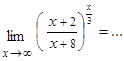







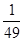
 означает, что
А)
означает, что
А)  ;
Б)
;
Б)  ;
В)
;
В)  ;
Г)
;
Г) 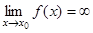 ;
Д)
;
Д)  .
.
 , если
, если  .
.

 , если
, если 

 найти
найти  .
.

 найти
найти  .
.
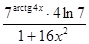
 найти
найти  в точке М (1;1).
в точке М (1;1).
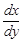 , если
, если 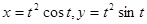 .
.

 , если
, если  .
.
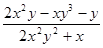
 , где
, где  . Найти
. Найти 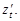

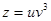 , где
, где  Найти
Найти 
 .
.

 в точках x =2 и x =5.
в точках x =2 и x =5.
 в точках
в точках  .
.
 .
.
 .
.

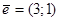 .
.
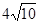

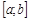 , то для
, то для  А)
А) 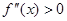 ,
,  ; Б)
; Б)  ,
, 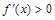 ;
В)
;
В) 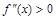 ,
,  .
.



